1. Types of data

• 学习目标
  辨认identify和使用不同种类的数据、用频率表frequency tables来展示收集的数据
• 关键词
  Primary data 主数据
  也可以叫一手数据，是通过我们自己去收集过来的
  Secondary data 次要数据
  也可以叫二手数据，二级数据，从其他人或者报纸上得到的数据，不是我们自己收集的数据

同时我们可以用其他的方式去描述我们的数据，比如离散数据 discrete data，离散数据表示的是单独的数据，比如6啊8啊什么的，比如说我们的宿舍号就属于离散数据

continuous data 连续数据，可以存在小数，表示连绵不断的数据，比如学生的年纪是17.66岁啊，去完成一项工作的时间是13.55秒啊这样子的

Frequency Table 频率表，能够给我们一种直接 immediate 的的数据的描述，最重要的是有一个频率在里面。

class intervals 组距，比如16-18,18-20，这些都是我们自己划分的组距
class boundaries 组界,正好像上面的组距中，16是最低数，18是最高数，这两个数字就是组界
class width 组宽，就是组距里最小数和最大数的差值
class frequency 组频率，频率表中最关键的一部分，表示该种数据在全部数据中的频率

• 建立数据表
  接下来学习如何建立construct 我们自己的频率表
  首先，我们需要去找到最大的数据和最小的数据，来决定范围Range，一般来说，最大数减去最小数就是范围
  其次，决定determine 组距的大小，可以自定义组距的大小，最终保持在5-10组数据是比较合理的
  然后，决定组宽，一定要注意组宽一定是相等的
  接下来，找到最小的数Lower Class Boundary，可以简称为LCB
  最后，就可以开始画表了

在草稿纸上可以使用这种方法来做笔记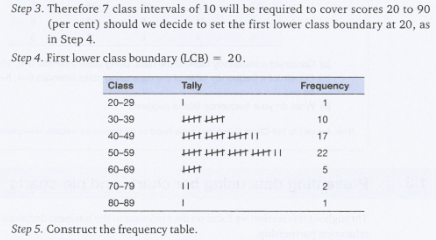

Charts，也是图表，这种图表大型数据那边用的比较多，同时他会展示数据之间的一些关系
Bar Chat条形图，这里我们主要学习简单的条形图，分为垂直Vertical条形图和水平horizontal条形图，主要给我们一种视觉的体验

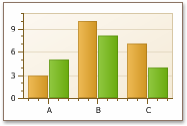
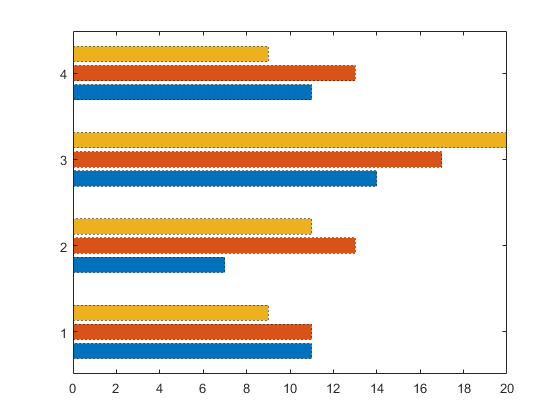
Component bar chat分段条形图，和刚才那个对比的话能够表示更多的信息，能有传达更多信息

Multiple bar chat群组条形图

Pie Chart饼图

Line Graphs线形图，主要展示的是一种趋势

Scatter Graphs散点图，用来展现一个变量，其实使用一个一个的点去表示变量在哪里

Histograms直方图，和条形图里的区别，就在于直方图里面的柱子是分开的，儿条形图里的是分开的

Frequency Polygons多边形
Frequency Curve曲线

在直方图中，如果把所有长方形的中间点连接起来，就可以得到一个频数分布直方图
但是当我们把长方形划分的足够小的时候，就能得到一个曲线，这个曲线就是频数曲线Frequency curve

2. Central Location

• Notation 符号

arithmetic mean 算数平均数
median 中位数
mode 众数
∑ = Greek letter sigma = sum of

举个栗子，如果有个人想创办一家公司，他找了8个专家来交谈，第一个交谈了4天，第二个交谈了2天，第三个交谈了5天，第四个交谈了4天，第五个交谈了2天，第六个交谈了1天，第七个交谈了4天，第八个交谈了3天，请问他一共交谈了多少天？
不得不说，这简直是个小学生级别的问题，真的是太难了
首先我们设
Xi = number of days
Fi = frequency with which Xi occurs
n = numbers of advisers
这样的话Xi 只有5种可能，就是最长的天数就是5天

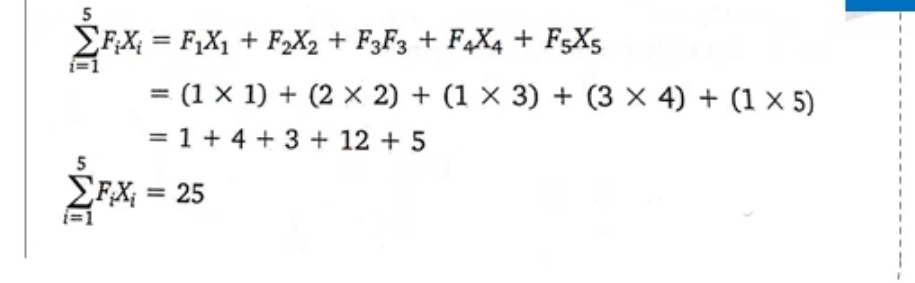
• Measures of Center Location 测量中心位置

average 平均
arithmetic mean 算数平均数
median 中位数
mode众数
grouped data未分组数据

所谓平均数，那很简单，就是总数除以个数
我们算出来的平均数并不是所给数据里的任意一个数
那如果是有频率的呢？

中位数就更不用说了
总数是单个数字的话就选取中间的那一个
如果是偶数的话就中间那两个数字除以二
不过要记得先排序

那么问题来了，如何计算已分组数据的平均数呢？

1. Find the median position 找到中位数所在的位置
2. Find the class interval in which the median observation fall找到中位数所在的对应的组是哪一个
3. assume that all items in this class interval are equally spaced 做一个假设，表明这个组里头所有的频率都是均匀分布的
4. Estimate the median 估计出中位数

没错我自己打这几行的时候也很蒙
还是举个栗子比较好
看看这个题目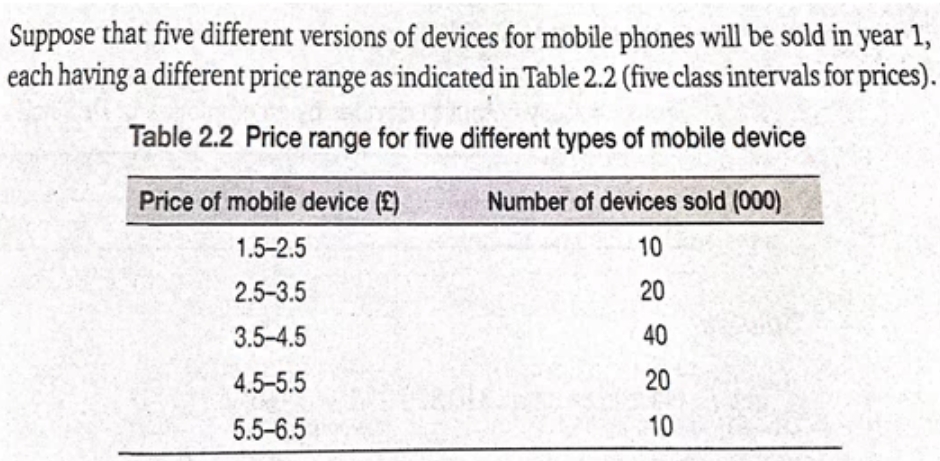

第一步：

这里是一个公式来的
如果样本容量是100的话
就用100+1除以二
一般都是50.5
中位数所在的位置就是50.5所对应的位置

下一步就是找到组距 class interval
我们可以先观察一下频率位于50的数大概在什么地方
从下往上数50的话，就是停留在3.5~4.5 频率为40 这个地方
这个时候使用下面这个公式:

LCB (Lower Class Boundary)最小的数据就是3.5（这里至区间内的）
那么这个时候组距(class interval)就是4.5-3.5 = 1
number of observations to median position 简单的来说就是用总的频率减去其他区间的频率，在这里就是50减去20减去10得到20.5
total number of observation in median class interval 算出这个区间的总频数，就是中位数所在区间的总频数，这里对应的数字是40
接下来就是愉快的代公式:
=3.5+1*(20.5/40)=4.01
那么得到的4.01就是中位数的值

• Mode 众数

接下来我们看看众数，这个简单的来说就是出现次数最多的数字(occurs most often),举个简单的栗子，5 7 7 9 这几个数字众数就是7.
那么如何找出已分组数据的众数呢？
找频率最大的那个呗，送分题

3. Making sense of data central location and dispersion

dispersion 分散
data central 数据位置

还是从实际案例入手吧
我们来看看人口样本
首先我们先了解一个概念：在大多数统计问题中，指定数量的测量值或数据（样本）是从更大的一组测量值（称为总体）中得出的。
用简单的小图来表示:

这里引入两个学术名词：
sample 样本
population 总量（大部分时候翻译为人口）

我们可以来思考一个问题
如果说有两个样本的直方图(histogram)看起来一样，但是又不全一样，你当然可以说他们是一样的，但是如何描述他们的不一样呢(degree of difference)？
为了解决这个问题，砖家们发明了一种东西，叫做 parameters（参数）,这个适用于大量测量相关的数字描述性（我也不懂，看看就行了），还有一个叫做statistics（统计）,是从样本度量中计算出的那些度量（不懂+1）

• Measures of Central Location 测量中心位置
  记得之前咱们学习过如何在已分组的数据中估计出中位数，那么如何测量中心位置捏
  瞧瞧这优秀的frequency tables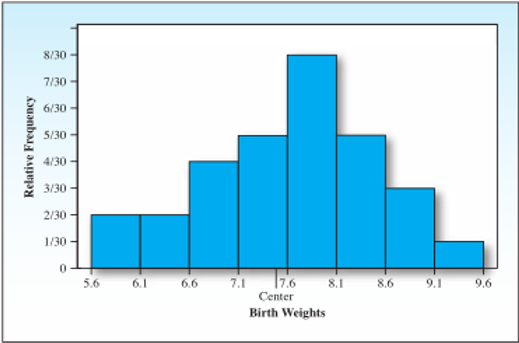
  

首先我们先来看看如何表示中位数
一般的，我们使用 x̅ 来表示样本平均值，念作 x-bar （就是酒吧的那个吧），用 μ 表示总体平均值，念作 mu （希腊字母），记得在上面讲过总体和样本的区别，这里就不再另外讲述了

• Dispersion 分散
  分散的话呢，就是有着相同中心的两个数据集，举个栗子吧：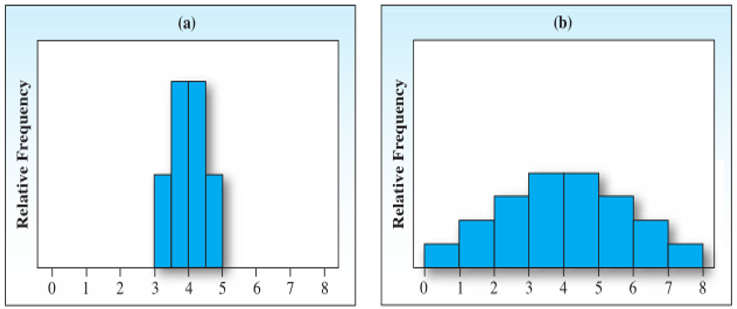
  
  

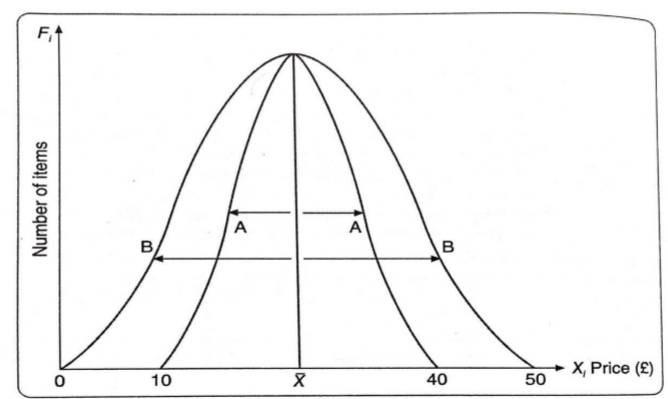
所以这里两个栗子，他们的数据的范围都不一样
Range 范围
所谓范围就是最大值减去最小值

接下来咱们去打篮球
记得在篮球里面有个玩意儿叫四分位 Interquartile range
在统计学里也有类似的概念
简单的来说，就是把一组数据分为25% , 50%, 75% 这3个关键位置，我们分别将这3个位置成为Q1 , Q2 , Q3 ,英文分别为 upper quartile , median quartile 和 lower quartile
还是用几张图来表示一下比较好

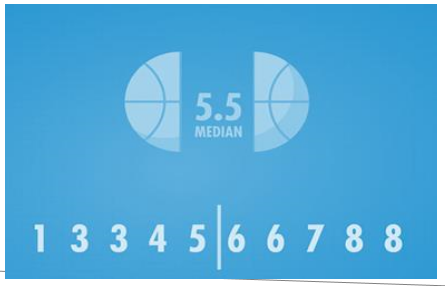
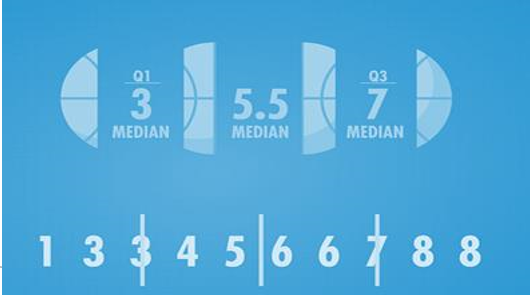
当然在表格中，也可以正常的表示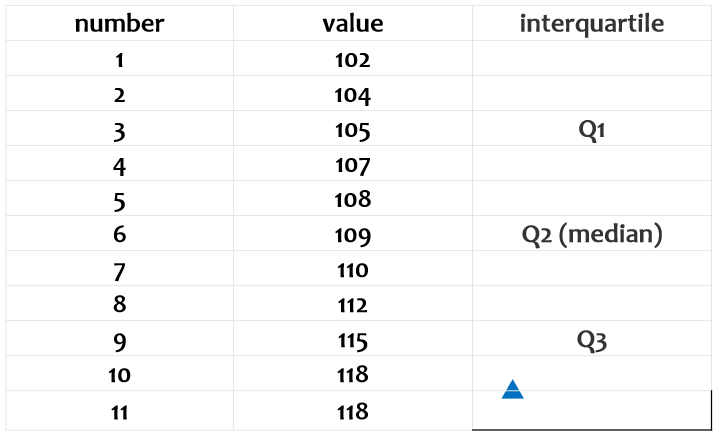

接下来来了解一个概念
叫做interquartile range 可以理解为四分位距
就是用Q3 - Q1 前提是Q3大于Q1
再加一个semi-interquartile range 半四分位距
就是把上面那个四分位距除以二就搞定了

下面引入一个概念，叫平均偏差 Mean Deviation ，简写为MD
说老实的，这玩意的定理一大堆但是非常难懂，不过举个栗子就很容易理解了
假如我们有3个数字，分别为4 , 5 , 6 , 为其定位X1=4 , X2=5 , X3=6
那么这三个数的平均数就是5（省略计算过程）（这里复习一下平均数的表示方法：x̅）
如果我们需要求这3个数的平局偏差（MD），就是：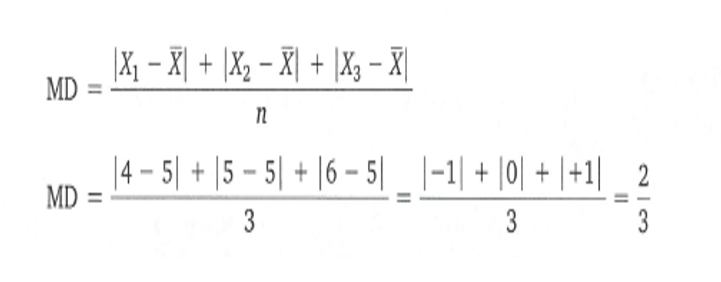

至于为什么要加个绝对值符号，那是因为在计算平均偏差的时候不考虑符号问题
你看前面那个就出现了个负一
不过完全不影响

variance 方差
反正我是记得在初中的时候，方差一直都是我的噩梦
因为算错一个数字就全部错完
那叫一个酸爽
在这里给出了小方法
简单的来说就是和初中的方法一样的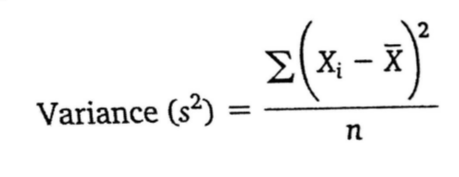

上面那个就是(每个数字减去平均数)的平方，再除以总数

那么问题来了，对于已经分好组的数据，如何求出他的方差呢？
这里有一个公式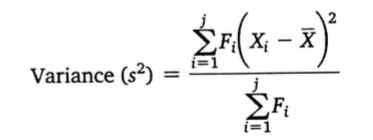

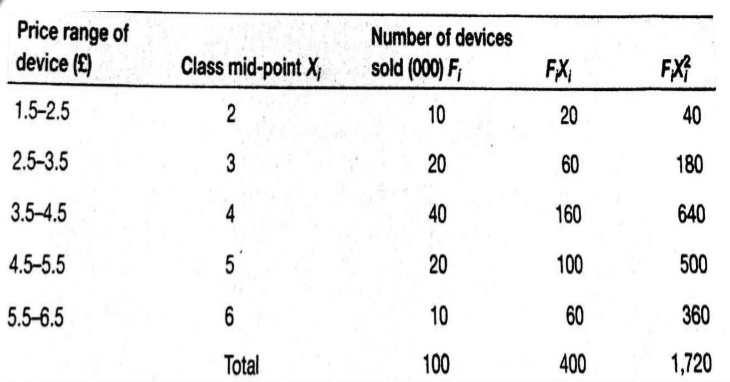
其中Fi是class frequency 频率
Xi是 class mid-point 中间值
x̅ 是 arithmetic mean 平均值
j 是 number of class intervals 组距
除此之外我们还有两条公式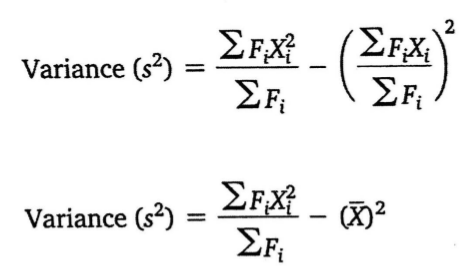

那么我们来看一个例题：

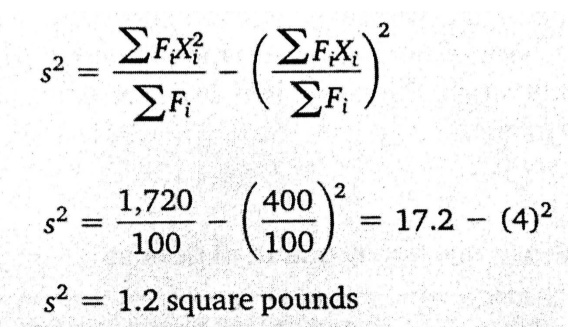
Cheapter 4: Regression correlation and time serise 回归和线性相关

上个学期我们已经学了一部分的线性关系，这次我们学习用一种方法去表示不同的变量之间的关系
今天学习的这种方法叫做最小二乘法

相关性分析的话，我们会使用最小二乘法来分析两个变量之间的关系
我们会用到两个变量去展现其关系
比如X是自变量 independent ，Y是因变量 dependent ,Y会随着X而改变
比如我们衣服的大小和我们衣服的成本是相关的，我们可以用X和Y来表示两者的关系

这里我们可以用一条式子来表示
Ŷ= mX + c
这里注意Y上面有个帽子一样的东西，我们将其读作Y-hat
那么这里面的每个字母都表示什么意思呢？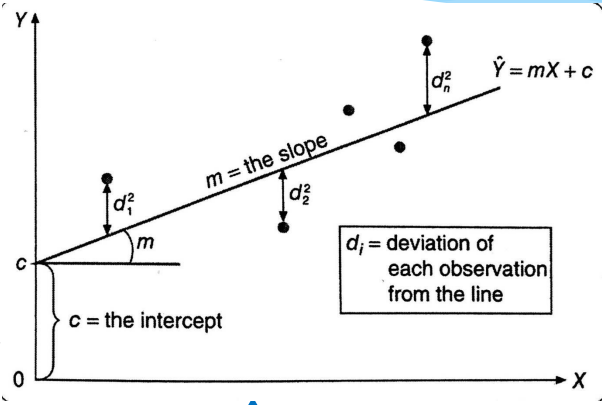

这里M代表截距，C代表斜率，也就是说当X的值为0的时候，C的值就是Y的值
这里我们发现不是所有点都在线上面，这时我们将观测点到线的距离叫做偏差 deviation
我们将其平方之后将其相加，当这个数字达到最小的时候就会出现一条唯一的线来显示他们的关系，
这种方法我们称之为最小二乘法

我们需要找这些