Chapter1: Introduction
我认为老师上课完全就是念PPT
PPT怎么写他就怎么念
他有时候也会用自己的话来说一遍
但是他用自己的话解释起来就像雅思的同义替换似的
换汤不换药
根本没有详细的例子来帮助理解
你看隔壁CC就喜欢举小狮子的例子来解释,简单易懂
最厉害的是,看视频的录制日期(有时候会录到桌面,右下角有日期),还是今年春节(2月份)的.......
讲道理我也不是要求这么高,但是我认为PPT只是留给学生做笔记用的一个工具
老师应该在PPT上写着重点内容,让学生能够记录下这些内容
而不是在PPT上写论文然后照着念
这不是上课,这看起来就像论文朗读大赛
我之前的笔记都是记录老师的解释的内容,因为我认为老师解释的内容跟有益于理解和记忆
但是这个老师完全没有什么值得留意的解释的内容
所以这个课堂笔记完全就是PPT上的内容
(摊手)
反正我也没这个能力去要求老师怎么上课
你看他甚至都用半年前的课件来上课
课程不按时(上课时间)开放,一定要凑整点才开放
课程观看时间仅限一天,过期就会锁起来
一个网课的优势就这样被他给整没了
真是不敢想象他来学校上课是个什么样子
反正我是很不喜欢这种上课方式的,但是没办法这个是必修课,就算用咖啡打吊瓶都得听下去
就这样吧
What is data?
Data is collection of facts and figures
Structure is the way of organizing so that easily readale
means computer can access data easily and use data easily
Data Structure is a way of collection and organizing data in such a way that we can perform operation on there data in an effective way. Data Structures is about rendering data elements in terms of some relationship, for batter origization and storage.
data structure is a form or organizing of data into structurally defined formate which may be readable or when ever it is required it may retrieve
说个人话,其实上面那一坨玩意我也看不懂
举个栗子来理解吧
假如我们需要存储一些数据,是人名+年龄
这里就涉及到String字符串和Intetger变量
那么我们如何同时存储这两个变量呢?
很简单,"Alex" 26, "Jacob" 31, balabala
你别看这玩意看似简单,但其实它真的很简单
不过这就是最基本的算法了
数据结构是一种收集和组织数据的方式,我们可以对其中的数据进行有效的操作。 数据结构是关于以某种关系呈现数据元素,以进行面糊组织和存储。
oh这见鬼的机翻
In simple terms, Data Structures are structures programmed to store ordered data, so that various operations can be performed on it easily. It represents the knowledge of data to be organized in memory.
It should be designed and implemented in such a way that it reduces the complexity and increases the efficiency
简而言之,数据结构是用编程来存储有序的数据,以便可以更加迅速和轻松地执行各种操作。它表示一种将内存中的数据排序要的知识。
我们在设计的时候应该使其有着更低的复杂程度并且提高效率
What we will study in data structure
As we defined data is collection of facts and figures: two main attributes which consist of either mathematical or logical or may be both
For the implementation of data structure, computer uses different computer language
Data structure required space and time to store data in memory
数据结构需要时间和空间将数据存储在内存中
Characteristics of a Data Structure 数据结构的特征
Correctness 正确性− Data structure implementation should implement its
interface correctly.
应该确保其正确性
Time Complexity 时间复杂度− Running time or the execution time of
operations of data structure must be as small as possible.
应该消耗更少的时间来完成工作
Space Complexity 空间复杂度− Memory usage of a data structure operation
should be as little as possible.
应该占用更少的内存来完成工作
*Program design depends crucially on how data is structuredfor use by the program:
Implementation of some operations may become easier or harder
Speed of program may dramatically decrease or increase
Memory used may increase or decrease
Debugging may be become easier or harder*
设计程序的时候主要取决于供程序使用的数据结构
- 易于还是难以操作和实施
- 程序的运行速速
- 内存的使用量
- 调试的难易程度
Mathematical description of an object with set of operations on the object. Useful building block.
用一组操作来描述的数学对象, 用于构建bolck。
- Algorithm 算法
A high level, language independent, description of a step-by-step process
高级和独立的语言,用于描述逐步说明的算法 - Data structure 数据结构
A specific family of algorithms for implementing an abstract data type.
用于实现特定算法的抽象数据类型 - Implementation of data structure 数据结构的实施
A specific implementation in a specific language 使用特定语言的特定实现(别说了这句话我也看不懂) - Field 字段
Field is a single elementary unit of information representing an attribute of an entity.
表示实体属性中的单个信息单元 - Record 记录
Record is a collection of field values of a given entity.
给定实体中字段集的集合 - File 文件
File is a collection of records of the entities in a given entity set.
给定实体集中实体记录的集合
*As we have discussed above, anything that can store data can be called as a data structure, hence Integer, Float, Boolean, Char etc., all are data structures. They are known as Primitive Data Structures. hence we also have some complex Data Structures, which are used to store large and connected data. Some example of Abstract Data
Structure are :
✓Linked List
✓Tree
✓Graph
✓Stack, Queue etc*
正如我们上面讨论的,任何可以存储数据的东西都可以称为数据结构,因此Integer,Float,Boolean,Char等都是数据结构。 它们被称为原始数据结构。 因此,我们还有一些复杂的数据结构,用于存储大型和连接的数据。 抽象数据结构的一些示例是:
✓链接列表
✓树
✓图
✓堆栈,队列等
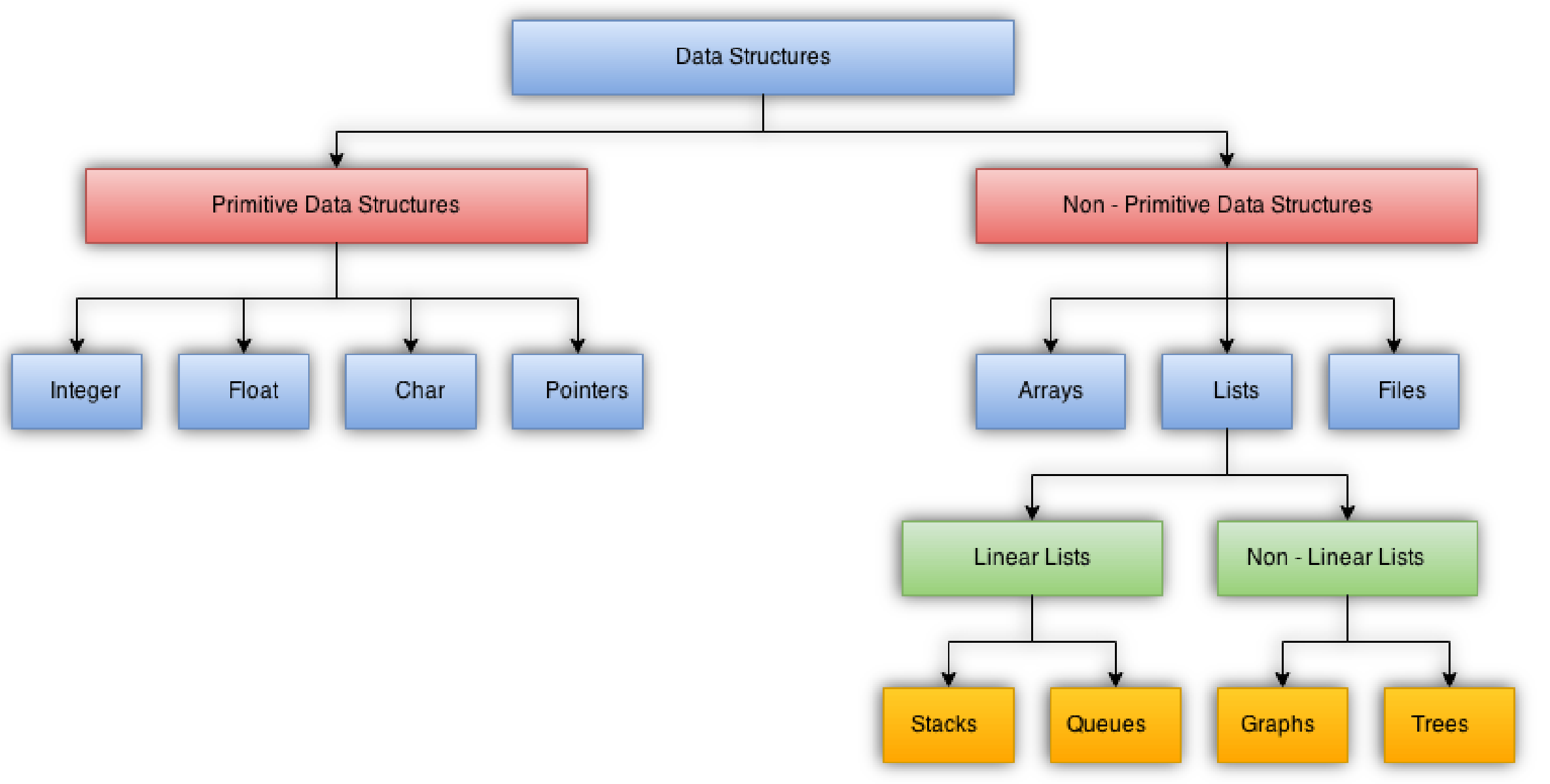
*Data structures can be broadly classified in two categories - linear structures and non-linear (hierarchical) structures.
▪ Arrays, linked lists, stacks, and queues are linear structures, while trees, graphs, heaps etc. are hierarchical structures.
▪Every data structure has its own strengths, and weaknesses.
▪Also, every data structure specially suits to specific problem types depending upon the operations performed and the data organization.*
数据结构可以大致分为两类-线性结构和非线性(分层)结构。
▪数组,链表,堆栈和队列是线性结构,而树,图,堆等是层次结构。
▪每个数据结构都有其优点和缺点。
▪此外,根据执行的操作和数据组织,每种数据结构都特别适合特定的问题类型。
*• Arrays are statically implemented data structures by some programming languages like C and C++;
• hence the size of this data structure must be known at compile time and cannot be altered at run time.
• But modern programming languages, for example, Java implements arrays as objects and give the programmer a way to alter the size of them at run time.
• Arrays are the most common data structure used to store data.*
数组
•数组是由某些编程语言(如C和C ++)静态实现的数据结构;
•因此,必须在编译时知道此数据结构的大小,并且不能在运行时更改它的大小。
•但是,例如现代编程语言,Java将数组实现为对象,并为程序员提供了一种在运行时更改数组大小的方法。
•数组是用于存储数据的最常见的数据结构。
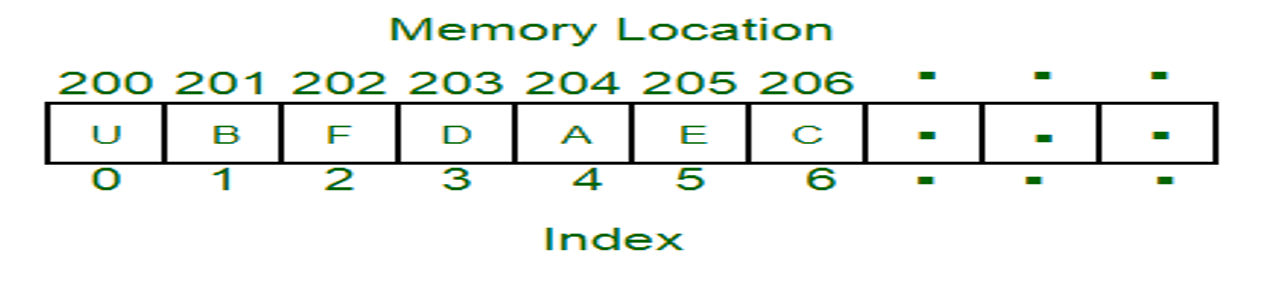
*• Linked list data structure provides better memory management than arrays.
• Because linked list is allocated memory at run time, so, there is no waste of memory.
• Performance wise linked list is slower than array because there is no direct access to linked list elements. • There are many flavors of linked list you will see: linear, circular, doubly, and doubly circular.*
•链表数据结构比数组提供更好的内存管理。
•因为链表是在运行时分配的内存,所以不会浪费内存。
•性能明智的链表比数组慢,因为无法直接访问链表元素。
•您会看到多种形式的链表:线性,圆形,双螺旋和双螺旋。
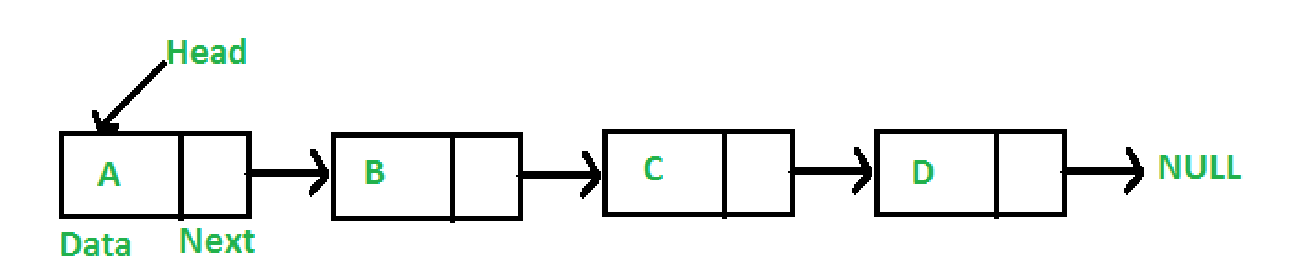
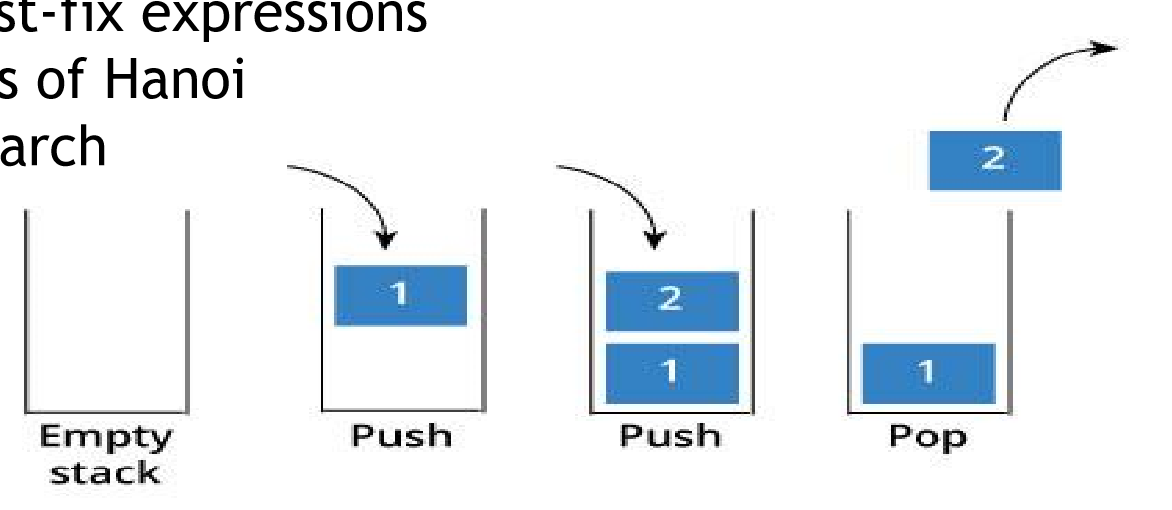
*Stack is a last-in-first-out strategy data structure; this means that the element stored in last will be removed first. Stack has specific but very useful applications; some of them are as follows:
- Solving Recursion - recursive calls are placed onto a stack, and removed from there once they are processed.
- Evaluating post-fix expressions
- Solving Towers of Hanoi
- Depth-first search*
堆栈是后进先出策略数据结构; 这意味着最后存储的元素将被首先删除。 堆栈具有特定但非常有用的应用程序; 其中一些如下:1.解决递归-递归调用被放置到堆栈上,并在处理后从堆栈中删除。
2.评估后缀表达式
3.解决河内塔楼
4.深度优先搜索
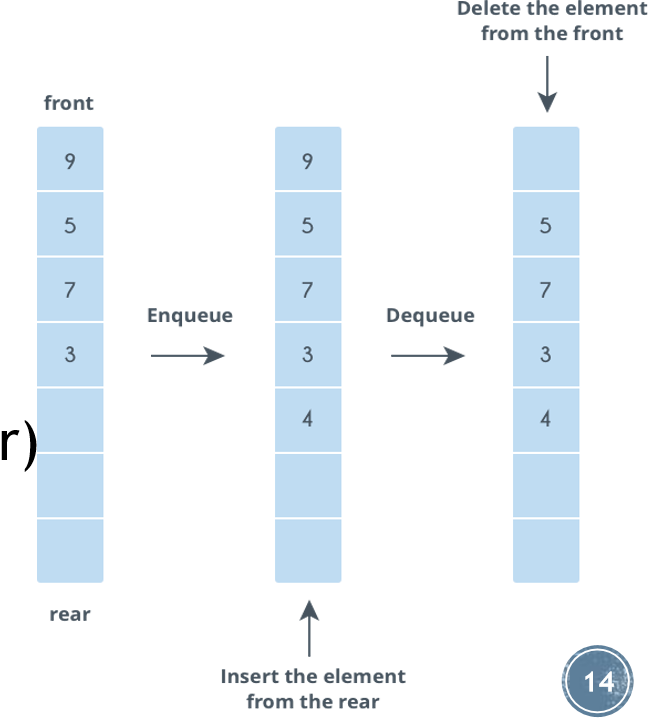
*Queue is a first-in-first-out data structure. The element that is added to the queue data structure first, will be removed from the queue first.
• Variants of queue data structure are :
1.Dequeue,
2.priority queue
3.circular queue.
• Queue has the following application uses:
1.Access to shared resources (e.g., printer)
2.Multiprogramming
3.Message queue*
队列是先进先出的数据结构。 首先添加到队列数据结构中的元素将首先从队列中删除。
•队列数据结构的变体是:
1.出队,
2.优先队列
3.循环队列。
•队列具有以下应用程序用途:
1.访问共享资源(例如,打印机)
2.多程序编程
3.消息队列
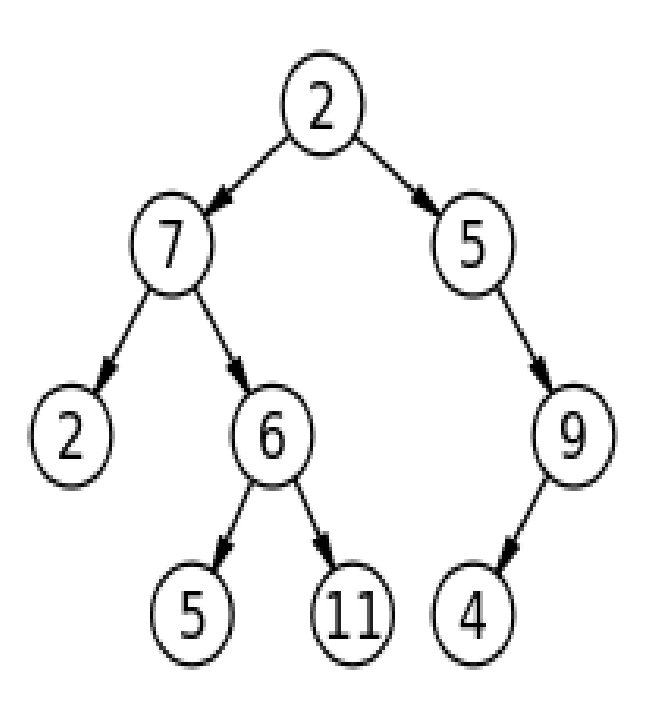
*• Tree is a hierarchical data structure.
• The very top element of a tree is called the root of the tree. Except the root element every element in a tree has a parent element, and zero or more children elements.
• All elements in the left sub-tree come before the root in sorting order, and all those in the right sub-tree come after the root.
• Tree is the most useful data structure when you have hierarchical information to store.*
•树是分层数据结构。
•树的最上层元素称为树的根。 除根元素外,树中的每个元素都有一个父元素,以及零个或多个子元素。
•左子树中的所有元素按排序顺序排在根之前,而右子树中的所有元素排在根之后。
•当您要存储分层信息时,树是最有用的数据结构。
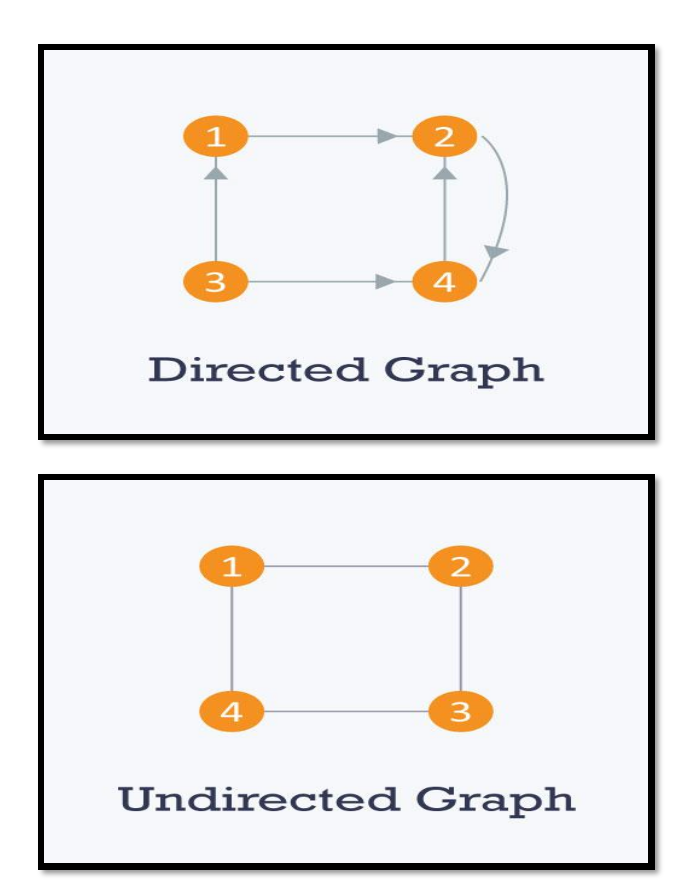
*• Graph is a networked data structure that connects a collection of nodes called vertices, by connections, called edges.
• An edge can be seen as a path or communication link between two nodes.
• These edges can be either directed or undirected.
• If a path is directed then you can move in one direction only, while in an undirected path the movement is possible in both directions.*
•图是一种联网的数据结构,它通过称为边的连接连接称为顶点的节点集合。
•边缘可视为两个节点之间的路径或通信链接。
•这些边缘可以是有向的也可以是无向的。
•如果路径是定向的,那么您只能在一个方向上移动,而在无方向的路径中,则可以在两个方向上移动。
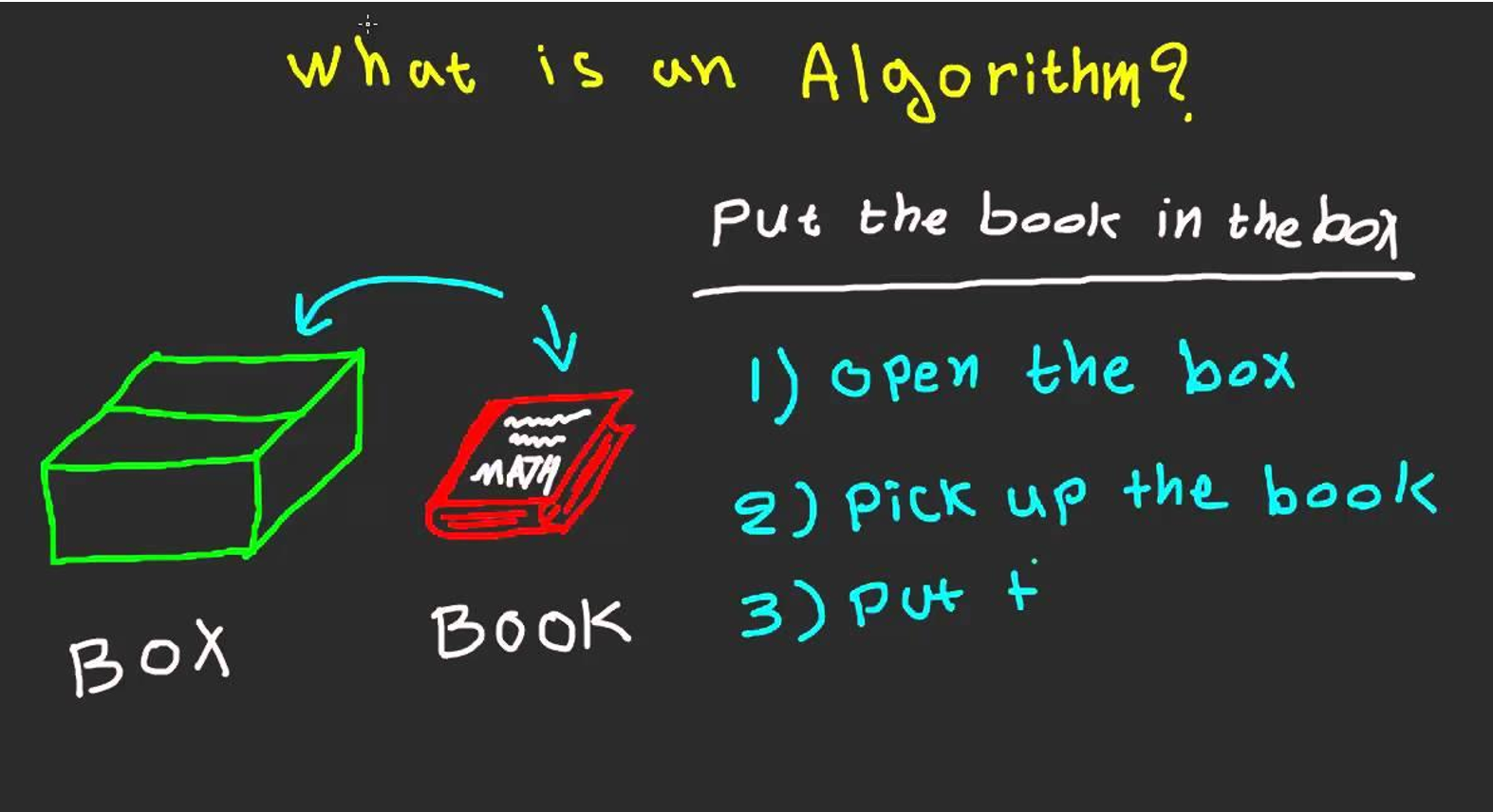
*• An algorithm is a step by step method of solving a problem.
• It is commonly used for data processing, calculation and other related computer and mathematical operations.
• An algorithm is also used to manipulate data in various ways, such as inserting a new data item, searching for a particular item or sorting an item.
• Algorithm is not the complete code or program, it is just the core logic(solution) of a problem, which can be expressed either as an informal high level description as pseudocode or using a flowchart*
•算法是解决问题的分步方法。
•它通常用于数据处理,计算以及其他相关的计算机和数学运算。
•算法还用于以各种方式操作数据,例如插入新数据项,搜索特定项或对项进行排序。
•算法不是完整的代码或程序,而只是问题的核心逻辑(解决方案),可以将其表示为伪代码的非正式高级描述或使用流程图
- Input- There should be 0 or more inputs supplied externally to the algorithm.
- Output- There should be at least 1 output obtained.
- Definiteness- Every step of the algorithm should be clear and well defined.
- Finiteness- The algorithm should have finite number of steps.
- Correctness- Every step of the algorithm must generate a correct output.*
每个算法必须满足以下属性:
1.输入-应该从外部向算法提供0个或多个输入。
2.输出-至少应获得1个输出。
3.确定性-算法的每个步骤都应明确并明确定义。
4.有限度-算法应具有有限数量的步骤。
5.正确性-算法的每一步都必须产生正确的输出。
*▪Algorithms must be free of doubt.
▪Algorithms should be efficient
▪Algorithms should be brief and compact to simplify verification of their correctness.
▪Algorithm should concern itself with one specific problem.
▪To express algorithm dealing with data structures, we will use a Java/Flowchart/PSEUDO language.*
▪算法必须毫无疑问。
▪算法应高效
▪算法应简洁明了,以简化对其正确性的验证。
▪算法应关注一个具体问题。
▪为了表达处理数据结构的算法,我们将使用Java / Flowchart / PSEUDO语言。
*• An algorithm is a detailed series of instructions for carrying out an operation or solving a problem.
• In a non-technical approach, we use algorithms in everyday tasks, such as a recipe to bake a cake or a do-it-yourself handbook.
• Technically, computers use algorithms to list the detailed instructions for carrying out an operation.
• For example, to compute an employee’s paycheck, the computer uses an algorithm. To accomplish this task, appropriate data must be entered into the system.
• In terms of efficiency, various algorithms are able to accomplish operations or problem solving easily and quickly.*
•算法是用于执行操作或解决问题的一系列详细指令。
•在非技术方法中,我们在日常任务中使用算法,例如烤蛋糕的食谱或自己动手的手册。
•从技术上讲,计算机使用算法列出执行操作的详细说明。
•例如,计算机使用一种算法来计算员工的薪水。 要完成此任务,必须在系统中输入适当的数据。
•就效率而言,各种算法能够轻松快速地完成操作或解决问题。
*▪Effectiveness
• simple
• can be carried out by pen and paper
▪Definiteness
• clear
• meaning is unique
▪Correctness
• give the right answer for all possible cases
▪Finiteness
• stop in reasonable time*
▪有效性
•简单
•可以用笔和纸进行
▪确定性
•清除
•意义是独一无二的
▪正确性
•针对所有可能的情况给出正确的答案
▪有限
•在合理的时间停止
*▪Design
• Divide & conquer, greedy, dynamic programming
▪Validation
• check whether it is correct
▪Analysis
• determine the properties of algorithm
▪Implementation
▪Testing
• check whether it works for all possible cases*
▪设计
•分而治之,贪婪,动态编程
▪验证
•检查是否正确
▪分析
•确定算法的属性
▪实施
▪测试
•检查它是否适用于所有可能的情况
Chapter2: Algorithm 算法
An algorithm is a detailed series of instructions for carrying out an operation or solving a problem.
算法是用于执行操作或解决问题的一系列详细指令。
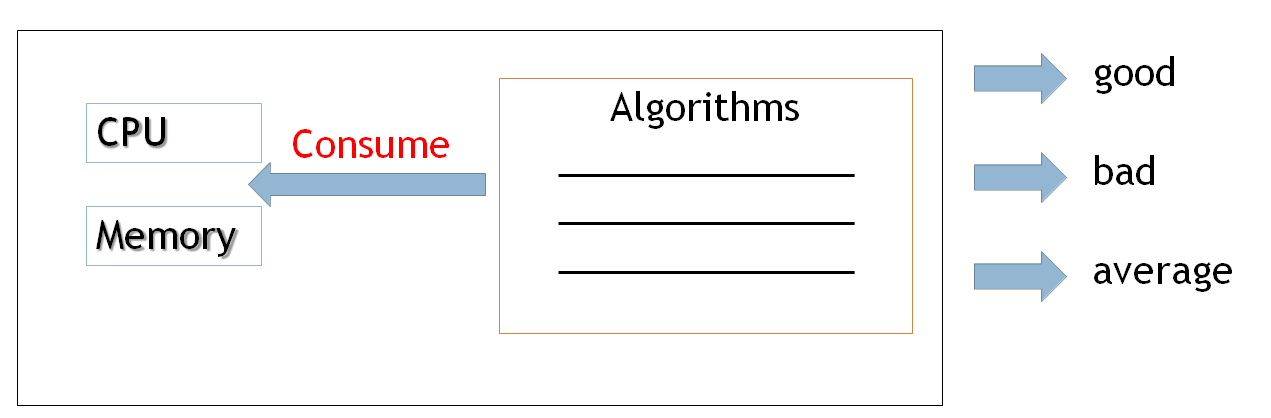
*Analysis of algorithm is the process of analyzing the problem-solving capability of the algorithm in terms of the time and size required (the size of memory for storage while implementation).
However, the main concern of analysis of algorithms is the required time or performance. Generally, we perform the following types of analysis −
- Best case
- Average case
- Worst case*
算法分析是从以下方面分析算法解决问题能力的过程:所需的时间和大小(实施时用于存储的内存大小)。
但是,算法分析的主要问题是所需的时间或性能。 通常,我们执行以下类型的分析-
- 最好的情况
- 平均情况
- 最坏的情况下
*Best case : fastest time to complete, with optimal inputs chosen.
Set of instruction which algorithm consumes less CPU and memory is called Best case.
Worst case : slowest time to complete, with more inputs chosen. Set of instruction which algorithm consumes more CPU and memory is called Worst case.
Average case : average time to complete.
set of instruction which algorithm consumes average CPU and memory is called Average case.*
最佳案例:最快的时间来完成,并选择最佳的输入。
一种算法消耗较少的CPU和内存的指令集称为“最佳情况”。
最坏的情况:完成时间最慢,选择了更多输入。 该算法消耗更多CPU和内存的指令集称为最坏情况。
平均情况:平均完成时间。
该算法消耗平均CPU和内存的指令集称为平均情况。
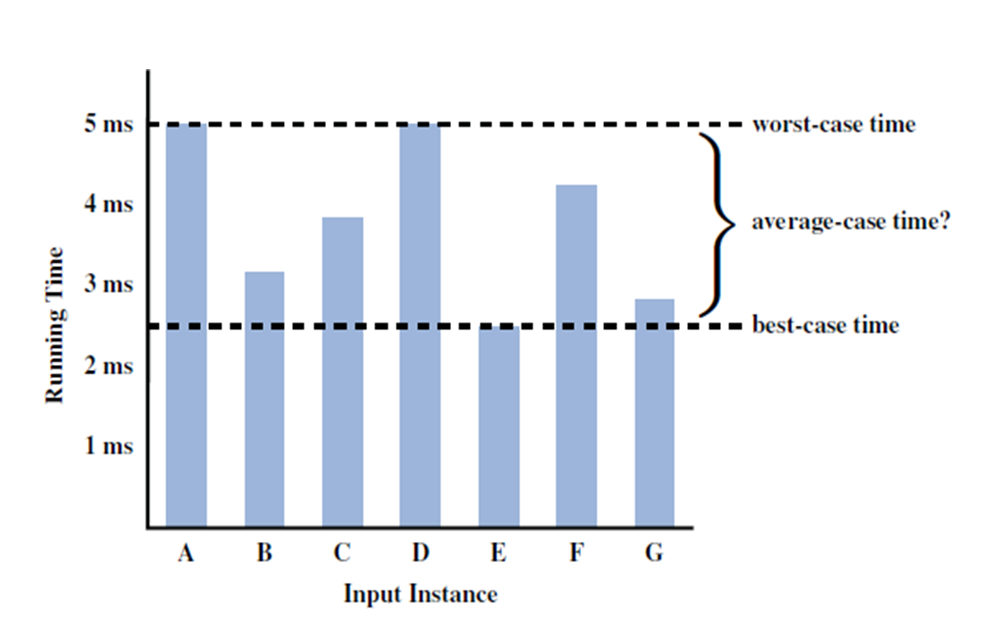
In computer science, linear search or sequential search is a method for finding an element within a list. It sequentially checks each element of the list until a match is found or the whole list has been searched.
在计算机科学中,线性搜索或顺序搜索是一种用于在列表中查找元素的方法。 它顺序检查列表中的每个元素,直到找到匹配项或搜索了整个列表。
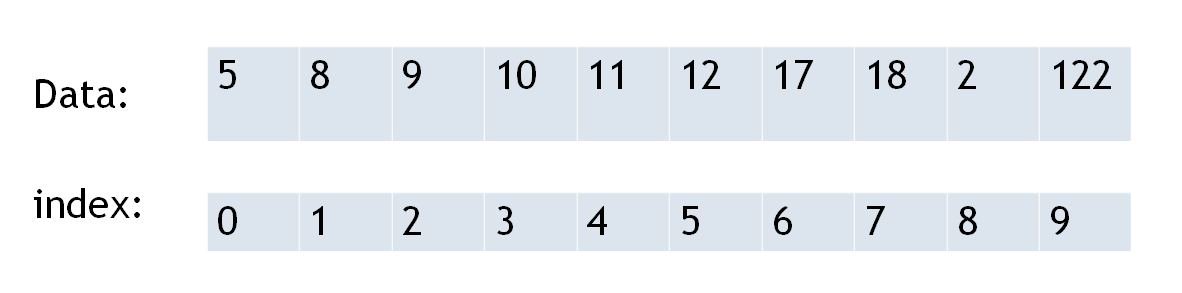
*Key = 12 which is at 5th index which means 6th element in list
Key = 100 Key element is not present in list
Search may be successful or may be unsuccessful depends upon the input and algorithm*
位置= 12 位于第5个索引处,表示列表中的第6个元素
位置= 100 列表中不存在元素
搜索可能成功还是失败取决于输入和算法
*Best case: searching for key element present at first index
What time it will take if I’m searching for first element in this example?
In this case first element is 5 then It will take constant time 1.
Best case time = 1 that is called constant O(1)
which means B(n) =O(1) // best case time for n element is order of 1
worst case: searching a key element present at last index
In this example 122 is last element which is present at last index
What is the time taken for searching that key element so I have to check all n elements .
worst case time : n
W(n)=O(n) // // worst case time for n element is order of n
*
最佳情况:搜索第一个索引处存在的关键元素
如果在此示例中搜索第一个元素,将花费什么时间?
在这种情况下,第一个元素为5,那么它将花费恒定的时间1。
最佳情况时间= 1,称为常数O(1)
这意味着B(n)= O(1)// n个元素的最佳情况时间为1的数量级
最坏的情况:搜索最后一个索引中存在的关键元素
在此示例中,122是出现在最后索引处的最后一个元素
搜索该关键元素花费的时间是多少,因此我必须检查所有n个元素。
最坏的情况:n
W(n)= O(n)// // n个元素的最坏情况时间是n的阶
average case: all possible case time / number of cases
平均案例:所有可能的案例时间/案例数
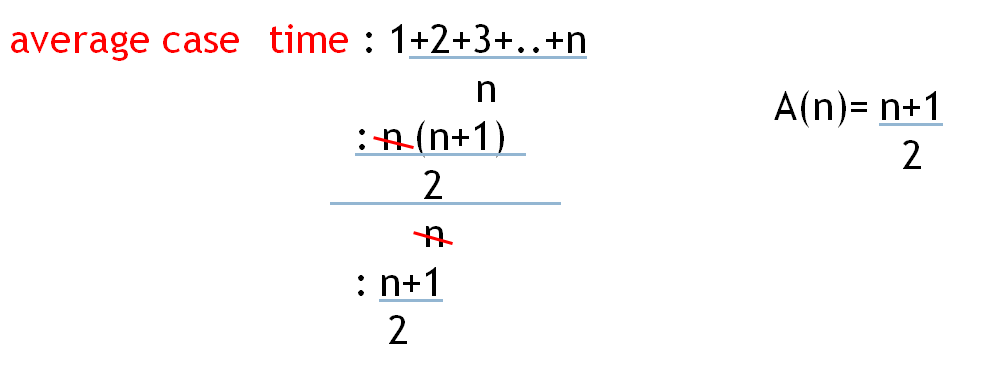
*Example: Design an algorithm to multiply the two numbers x and y and display the result in z.
Step 1 START
Step 2 declare three integers x, y & z
Step 3 define values of x & y
Step 4 multiply values of x & y
Step 5 store the output of step 4 in z
Step 6 print z
Step 7 STOP*
示例:设计一种算法以将两个数字x和y相乘并在z中显示结果。
步骤1开始
第2步声明三个整数x,y和z
步骤3定义x和y的值
步骤4将x和y的值相乘
步骤5将步骤4的输出存储在z中
步骤6列印z
步骤7停止
*Alternatively the algorithm can be written as ?
Step 1 START MULTIPLY
Step 2 get values of x & y
Step 3 z← x * y
Step 4 display z
Step 5 STOP*
另外,算法可以写成?
第1步开始
步骤2获得x和y的值
步骤3 z←x * y
步骤4显示z
步骤5停止
Every algorithm needs a process in order to be created and utilized. Described below are the phases of algorithm analysis and design:
每个算法都需要一个过程才能被创建和利用。 以下是算法分析和设计的阶段:

*This step is much more difficult than it appears.
In the following discussion, the word client refers to someone who wants to find a solution to a problem, and the word developer refers to someone who finds a way to solve the problem.
The developer must create an algorithm that will solve the client's problem.*
这一步比看起来要困难得多。
在下面的讨论中,“客户”一词是指想要找到问题的解决方案的人,而“开发者”一词是指找到解决问题的方法的人。
开发人员必须创建一种可以解决客户问题的算法。
*The client is responsible for creating a description of the problem, but this is often the weakest part of the process.
It's quite common for a problem description to suffer from one or more of the following types of defects:
the description relies on unstated assumptions,
the description is ambiguous,
the description is incomplete, or
the description has internal contradictions.*
客户负责创建问题的描述,但这通常是过程中最薄弱的部分。
问题描述遭受以下一种或多种类型的缺陷是很常见的:
该描述基于未陈述的假设,
描述不明确,
说明不完整,或
该说明存在内部矛盾。
*- The purpose of this step is to determine both the starting and ending points for solving the problem.
- This process is analogous to a mathematician determining what is given and what must be proven.
- A good problem description makes it easier to perform this step.*
此步骤的目的是确定解决问题的起点和终点。
此过程类似于确定给定和必须证明的数学家。
良好的问题描述可以使执行此步骤更加容易。
*When determining the starting point, we should start by seeking answers to the following questions:
- What data are available?
- Where is that data?
- What formulas pertain to the problem?
- What rules exist for working with the data?
- What relationships exist among the data values?*
在确定起点时,我们应该首先寻求以下问题的答案:
- 有哪些可用数据?
- 该数据在哪里?
- 什么公式与问题有关?
- 存在哪些数据处理规则?
- 数据值之间存在什么关系?
When determining the ending point, we need to describe the characteristics of a solution. In other words, how will we know when we're done? Asking the following questions often helps to determine the ending point.
- What new facts will we have?
- What items will have changed?
- What changes will have been made to those items?
- What things will no longer exist?
确定终点时,我们需要描述解决方案的特征。 换句话说,我们怎么知道什么时候完成? 提出以下问题通常有助于确定终点。
- 我们将拥有哪些新事实?
- 哪些项目将会改变?
- 这些项目将进行哪些更改?
- 什么东西将不再存在?
An algorithm is a plan for solving a problem, but plans come in several levels of detail.
It's usually better to start with a high-level algorithm that includes the major part of a solution, but leaves the details until later.
We can use an everyday example to demonstrate a high- level algorithm.
算法是解决问题的计划,但是计划有多个层次。
通常最好从包含解决方案主要部分的高级算法开始,但将细节保留到稍后。
我们可以使用一个日常示例来演示高级算法。
Problem: I need a send a birthday card to my brother, Mark.
Analysis: I don't have a card. I prefer to buy a card rather than make one myself.
High-level algorithm:
- Go to a store that sells greeting cards
- Select a card
- Purchase a card
- Mail the card
问题:我需要给我的兄弟马克寄一张生日贺卡。
分析:我没有卡。 我宁愿买一张卡,也不愿自己做一张。
高级算法:
- 去卖贺卡的商店
- 选择一张卡
- 购买卡
- 邮寄卡
This algorithm is satisfactory for daily use, but it lacks details that would have to be added were a computer to carry out the solution. These details include answers to questions such as the following.
"Which store will I visit?"
"How will I get there: walk, drive, ride my bicycle, take the bus?" "What kind of card does Mark like: humorous, sentimental, risk?" These kinds of details are considered in the next step of our process.
该算法对于日常使用是令人满意的,但是它缺少一些细节,如果要执行该解决方案,则必须添加一些细节。 这些详细信息包括对以下问题的解答。
我会去哪家商店?
“我将如何到达那里:走路,开车,骑自行车,乘公共汽车?” “马克喜欢什么样的牌:幽默,感性,冒险?” 这些细节将在我们流程的下一步中进行考虑。
A high-level algorithm shows the major steps that need to be followed to solve a problem. Now we need to add details to these steps, but how much detail should we add? Unfortunately, the answer to this question depends on the situation.
We have to consider who (or what) is going to implement the algorithm and how much that person (or thing) already knows how to do.
高级算法显示解决问题需要遵循的主要步骤。 现在我们需要在这些步骤中添加细节,但是我们应该添加多少细节? 不幸的是,这个问题的答案取决于情况。
我们必须考虑谁(或什么)将实施该算法,以及该人(或事物)已经知道如何执行该算法。
For example :
If someone is going to purchase Mark's birthday card on my behalf, my instructions have to be adapted to whether or not that person is familiar with the stores in the community and how well the purchaser known my brother's taste in greeting cards.
When our goal is to develop algorithms that will lead to computer programs, we need to consider the capabilities of the computer and provide enough detail.
so that someone else could use our algorithm to write a computer program that follows the steps in our algorithm.
例如 :
如果有人要代表我购买Mark的生日贺卡,则必须对我的指示进行调整,以适应该人是否熟悉社区中的商店以及购买者对贺卡中我兄弟的口味的了解程度。
当我们的目标是开发能够生成计算机程序的算法时,我们需要考虑计算机的功能并提供足够的细节。
这样其他人就可以使用我们的算法来编写遵循我们算法中步骤的计算机程序。
The final step is to review the algorithm. What are we looking for?
First, we need to work through the algorithm step by step to determine whether or not it will solve the original problem.
Once we are satisfied that the algorithm does provide a solution to the problem, we start to look for other things.
最后一步是审查算法。 我们在找什么?
首先,我们需要逐步研究算法,以确定它是否可以解决原始问题。
一旦我们对算法确实提供了解决问题的方法感到满意,我们便开始寻找其他东西。
The following questions are typical of ones that should be asked whenever we review an algorithm. Asking these questions and seeking their answers is a good way to develop skills that can be applied to the next problem.
Does this algorithm solve a very specific problem or does it solve a more general problem? If it solves a very specific problem, should it be generalized?
- For example, an algorithm that computes the area of a circle having radius 5.2 meters (formula π*5.22) solves a very specific problem,
- but an algorithm that computes the area of any circle (formula π*R2) solves a more general problem.
以下问题是每当我们审查算法时应提出的典型问题。 提出这些问题并寻求答案是发展可应用于下一个问题的技能的好方法。
该算法是解决非常具体的问题还是解决更一般的问题? 如果它解决了非常具体的问题,是否应该将其概括化?
- 例如,一种计算半径为5.2米(公式π* 5.22)的圆的面积的算法解决了一个非常具体的问题,
- 但是可以计算任何圆的面积的算法(公式π* R2)解决了一个更一般的问题。
Can this algorithm be simplified?
- One formula for computing the perimeter of a rectangle is:
length + width + length + width - A simpler formula would be:
2.0 * (length + width)
Is this solution similar to the solution to another problem? How are they alike? How are they different?
For example, consider the following two formula:
- Rectangle area = length * width
- Triangle area = 0.5 base height
可以简化此算法吗?
- 计算矩形周长的一个公式是:
长+宽+长+宽 - 一个简单的公式是:
2.0 *(长+宽)
该解决方案是否类似于另一个问题的解决方案? 他们怎么样? 它们有何不同?
例如,考虑以下两个公式:
- 矩形面积=长*宽
- 三角形面积= 0.5 基础高度
A computer scientist measures an algorithm's efficiency in terms of its time complexity and space complexity by using complexity functions to abstract implementation and runtime environment details.
Complexity functions reveal the variance in an algorithm's time and space requirements based on the amount of input data:
- A time-complexity function measures an algorithm's time complexity--meaning how long an algorithm takes to complete.
- A space-complexity function measures an algorithm's space complexity--meaning the amount of memory overhead required by the algorithm to perform its task.
计算机科学家通过使用复杂度函数来抽象实现和运行时环境细节,从而根据时间复杂度和空间复杂度来衡量算法的效率。
复杂度函数根据输入数据量揭示算法的时间和空间要求的方差:
- 时间复杂度函数可衡量算法的时间复杂度,即算法完成所需的时间。
- 空间复杂度函数衡量算法的空间复杂度-意味着算法执行其任务所需的内存开销量。
- Time complexity of an algorithm represents the amount of time required by the algorithm to run to completion.
- Time requirements can be defined as a numerical function T(n), where T(n) can be measured as the number of steps, provided each step consumes constant time.
- For example, addition of two n-bit integers takes n steps. Consequently, the total computational time is T(n) = c ∗ n,
- where c is the time taken for the addition of two bits. Here, we observe that T(n) grows linearly as the input size increases.
- 算法的时间复杂度表示算法运行完成所需的时间。
- 时间要求可以定义为数值函数T(n),其中T(n)可以作为步数来衡量,前提是每一步都消耗恒定的时间。
- 例如,两个n位整数相加需要n步。 因此,总的计算时间为T(n)= c ∗ n,
- 其中c是两个位相加所花费的时间。 在这里,我们观察到T(n)随着输入大小的增加而线性增长。
It's fairly easy to choose a time-complexity function for the array- printing example, but it can be more difficult to find this function for more complicated algorithms. Use the following rules-of-thumb to simplify this task:
- Algorithms with single loops are typically linear--their time- complexity functions are specified in terms of n.
- Algorithms with two nested loops are typically quadratic--their time-complexity functions are specified in terms of n2.
- Algorithms with a triply-nested loop are typically cubic--their time- complexity functions are specified in terms of n3.
- This pattern continues with quadruple and higher nested loops.
为阵列打印示例选择时间复杂度函数相当容易,但是对于更复杂的算法,找到该函数可能会更加困难。 使用以下经验法则可以简化此任务:
- 具有单循环的算法通常是线性的-它们的时间复杂度函数以n表示。
- 具有两个嵌套循环的算法通常是二次的-它们的时间复杂度函数以n2表示。
- 具有三重嵌套循环的算法通常是三次的-它们的时间复杂度函数以n3的形式指定。
- 此模式以四个和更高的嵌套循环继续。
Space complexity of an algorithm represents the amount of memory space required by the algorithm in its life cycle. The space required by an algorithm is equal to the sum of the following two components
- A fixed part that is a space required to store certain data and
variables, that are independent of the size of the problem. For example, simple variables and constants used, program size, etc.
- A variable part is a space required by variables, whose size depends on the size of the problem. For example, dynamic memory allocation, recursion stack space, etc.
算法的空间复杂度表示算法在其生命周期中所需的存储空间量。 算法所需的空间等于以下两个组成部分的总和。o固定部分是存储某些数据所需的空间,
- 变量,与问题的大小无关。 例如,使用的简单变量和常量,程序大小等。
- 变量部分是变量所需的空间,其大小取决于问题的大小。 例如,动态内存分配,递归堆栈空间等。
For calculating the space complexity, we need to know the value of memory used by different type of datatype variables, which generally varies for different operating systems, but the method for calculating the space complexity remains the same.
为了计算空间复杂度,我们需要了解不同类型的数据类型变量使用的内存值,该值通常随不同的操作系统而有所不同,但是计算空间复杂度的方法保持不变。
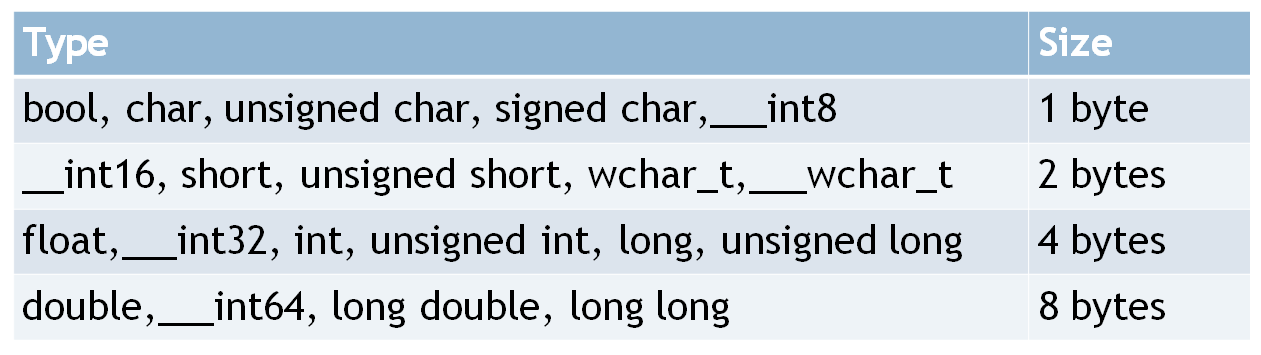
Now let's learn how to compute space complexity by taking a few examples:
现在,让我们学习如何通过采取一些例子来计算空间复杂度:

In the above expression, variables a, b, c and z are all integer types, hence they will take up 4 bytes each, so total memory requirement will be (4(4) + 4) = 20 bytes, this additional 4 bytes is for return value. And because this space requirement is fixed for the above example, hence it is called Constant Space Complexity.
在上面的表达式中,变量a,b,c和z都是整数类型,因此它们每个都占用4个字节,因此总内存需求为(4(4)+ 4)= 20字节,另外4个字节为 返回值。 并且由于对于上面的示例此空间要求是固定的,因此它被称为恒定空间复杂度。
Let's have another example, this time a bit complex one,
让我们再举一个例子,这次有点复杂,

in the above code, 4*n bytes of space is required for the array a[] elements. 4 bytes each for x, n, i and the return value.
在上面的代码中,数组a []元素需要4 * n字节的空间。 x,n,i和返回值各4个字节。
Hence the total memory requirement will be (4n + 16), which is increasing linearly with the increase in the input value n, hence it is called as Linear Space Complexity.
因此,总存储需求为(4n + 16),随着输入值n的增加而线性增加,因此称为线性空间复杂度。
Chapter3: Recursion 递归
It is the concept of defining a method that makes a call to itself and the call is termed as a recursive call.
Recursion is a technique to divide the problem into subproblems of the same type.
Recursion reduces the performance of program as it takes time to shift the control to a function and getting it back to the caller. It takes much space as recursion forward (winding). A termination statement is properly set to overcome from the problem of stack overflow.
定义方法的概念是对自身进行调用,该调用称为递归调用。
递归是一种将问题划分为相同类型的子问题的技术。
递归会降低程序的性能,因为将控件转移到函数并将其返回给调用者需要花费时间。 递归向前(缠绕)会占用很多空间。 正确设置了终止语句,以克服堆栈溢出的问题。
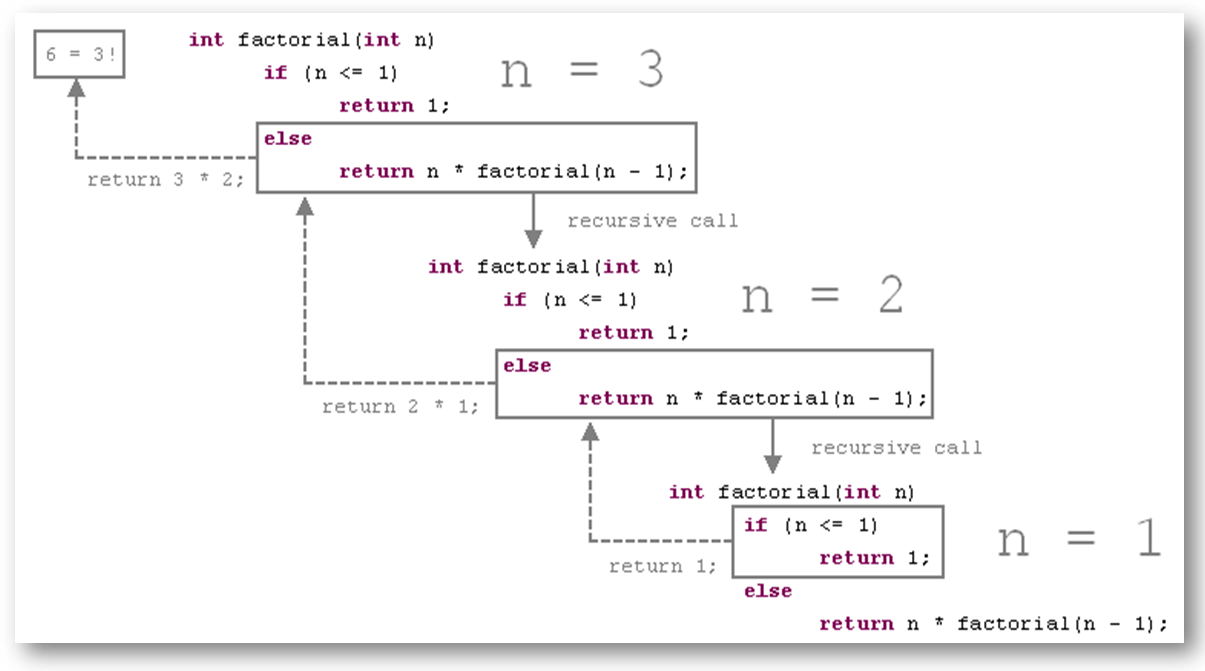
class Factorial {
static int factorial( int n ) {
if (n != 0)
return n * factorial(n-1); // recursive call
else
return 1;
}
public static void main(String[] args) {
int number = 3, result;
result = factorial(number);
System.out.println(number + " factorial = " + result);
}
}
When you run above program, the output will be: 3 factorial = 6
当您运行上述程序时,输出将是: 3 factorial = 6
There are n people in a room. If each person shakes hands once with every other person. What is the total number h(n) of handshakes?
一个房间里有n个人。 如果每个人都与其他人握手一次。 握手的总数h(n)是多少?
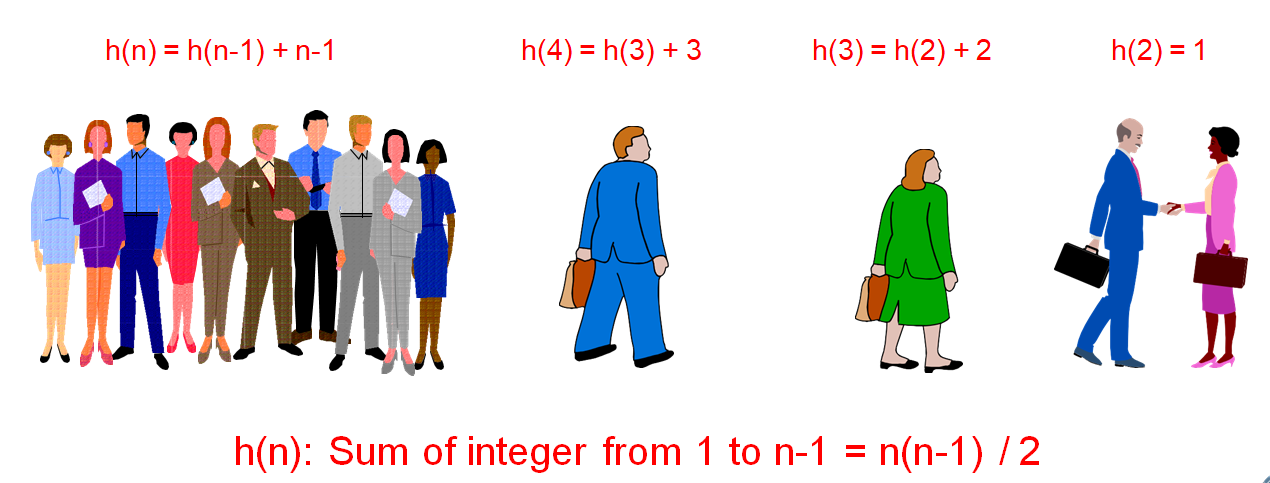
In general, we can express the factorial function as follows:
n! = n * (n-1)!
Is this correct? Well… almost.
The factorial function is only defined for positive integers. So we should be a bit more precise:
n! = 1 (if n is equal to 1)
n! = n * (n-1)! (if n is larger than 1)
通常,我们可以将阶乘函数表示为:
n! = n *(n-1)!
它是否正确? 好吧...差不多。
阶乘函数仅针对正整数定义。 因此,我们应该更精确一些:
n! = 1 (if n is equal to 1)
n! = n * (n-1)! (if n is larger than 1)
A recursive function can go infinite like a loop. To avoid infinite running of recursive function, there are two properties that a recursive function must have −
- Base criteria − There must be at least one base criteria or condition, such that, when this condition is met the function stops calling itself recursively.
- Progressive approach − The recursive calls should progress in such a way that each time a recursive call is made it comes closer to the base criteria.
递归函数可以像循环一样无限循环。 为了避免无限运行递归函数,递归函数必须具有两个属性-
- 基本标准-必须至少有一个基本标准或条件,以便在满足此条件时,该函数停止递归调用自身。
- 渐进方法-递归调用应以每次进行递归调用时都更接近基本标准的方式进行。
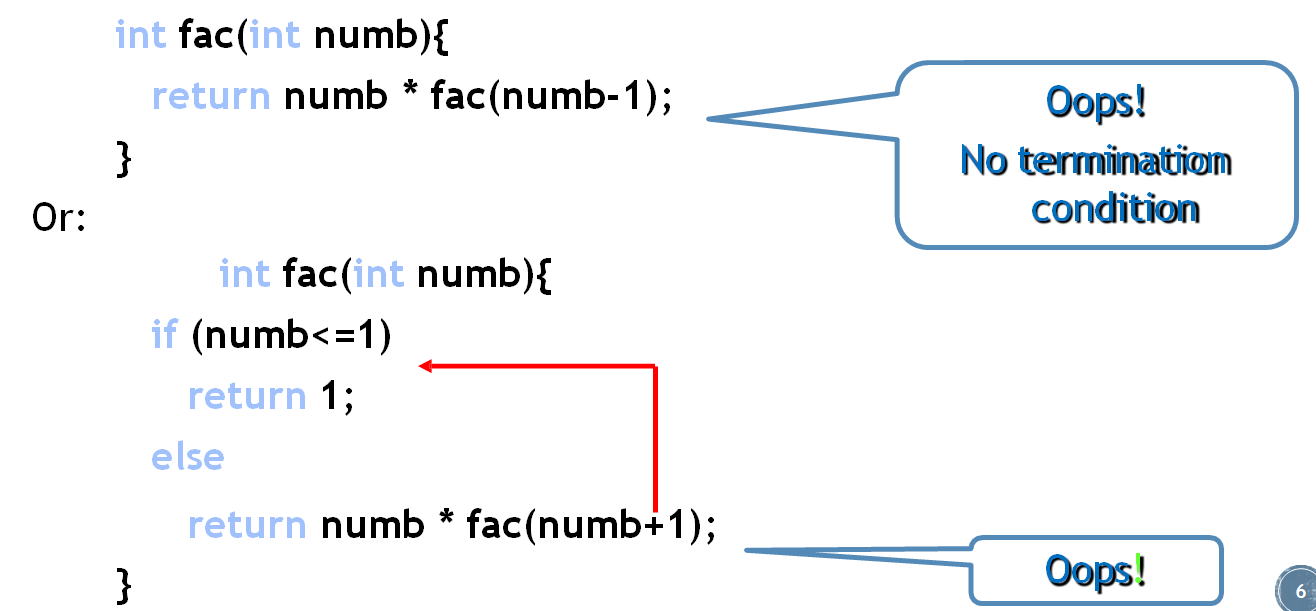
Similarly, if we use recursion we must be careful not to create an infinite chain of function calls:
同样,如果我们使用递归,则必须注意不要创建无限的函数调用链:
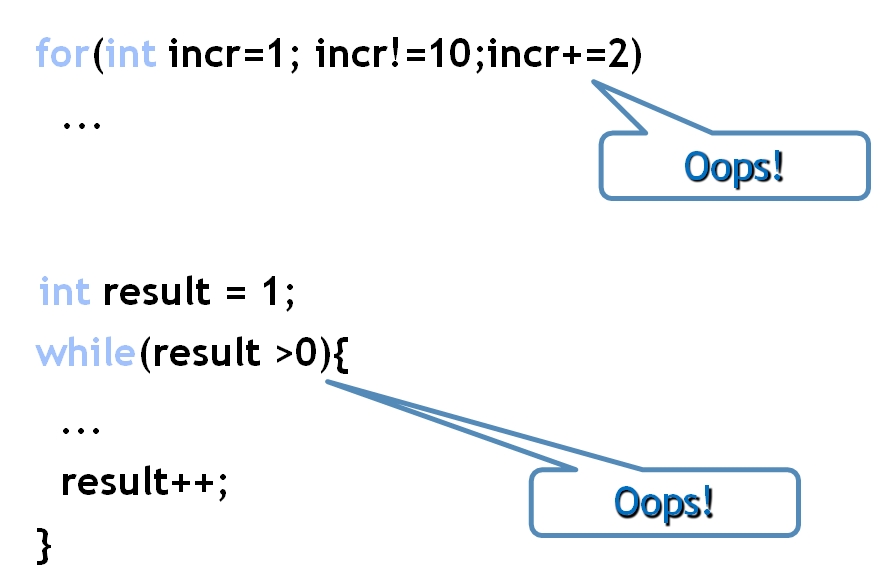
If we use iteration, we must be careful not to create an infinite loop by accident:
如果使用迭代,则必须小心不要意外创建无限循环:
In the above program, recurse() method is called from inside the main method at first (normal method call).
Also, recurse() method is called from inside the same method, recurse(). This is a recursive call.
在上面的程序中,首先从main方法内部调用recurse()方法(正常方法调用)。
同样,从相同的方法recurse()内部调用recurse()方法。 这是一个递归调用。
The recursion continues until some condition is met to prevent it from execution. If not, infinite recursion occurs.
递归继续进行,直到满足某些条件以阻止其执行。 否则,将发生无限递归。

to prevent infinite recursion, if...else statement (or similar approach) can be used
为了防止无限递归,如果可以使用...其他语句(或类似方法)
As we discoursed in the previous sessions, recursion is a process of executing a statement or multiple statements repeatedly by calling a function itself.
Recursion reduces the performance of program as it takes time to shift the control to a function and getting it back to the caller.
In this session, we will discourse different ways of building recursion. Some of which are already discoursed in the previous sessions.
- Linear recursion
- Binary recursion
- Mutual recursion
正如我们在前几节中讨论的那样,递归是通过调用函数本身重复执行一个或多个语句的过程。
递归会降低程序的性能,因为将控件转移到函数并将其返回给调用者需要花费时间。
在本节中,我们将讨论构建递归的不同方法。 在先前的会议中已经讨论了其中的一些。
- 线性递归
- 二进制递归
- 相互递归
It is the most commonly used recursion, where a function calls itself in simple manner and a terminating condition is used to terminate the recursion.
Forwarding recursion is called winding and getting the control back to the caller is called unwinding.
它是最常用的递归,其中函数以简单的方式调用自身,并且使用终止条件来终止递归。
转发递归称为结束,将控件返回给调用者称为取消结束。
long factorial(int n)
{
int f;
if(n==1) /* terminating condition */ return 1;
f=n*factorial(n-1); /* calling function itself */ return f;
}
It is a type of recursion where function is called twice instead once in the recursive functions.
When an algorithm makes two recursive calls, we say that it uses binary recursion. Binary recursion is useful where we can think of dividing the problem in hand in almost equal halves.
This type of recursive functions were used in implementing Towers of Hanoi, Binary search and Quick sort.
这是一种递归,其中函数在递归函数中被调用两次,而不是一次。
当一个算法进行两次递归调用时,我们说它使用二进制递归。 当我们可以考虑将问题分成几乎相等的一半时,二进制递归很有用。
这种类型的递归函数用于实现河内塔,二进制搜索和快速排序。
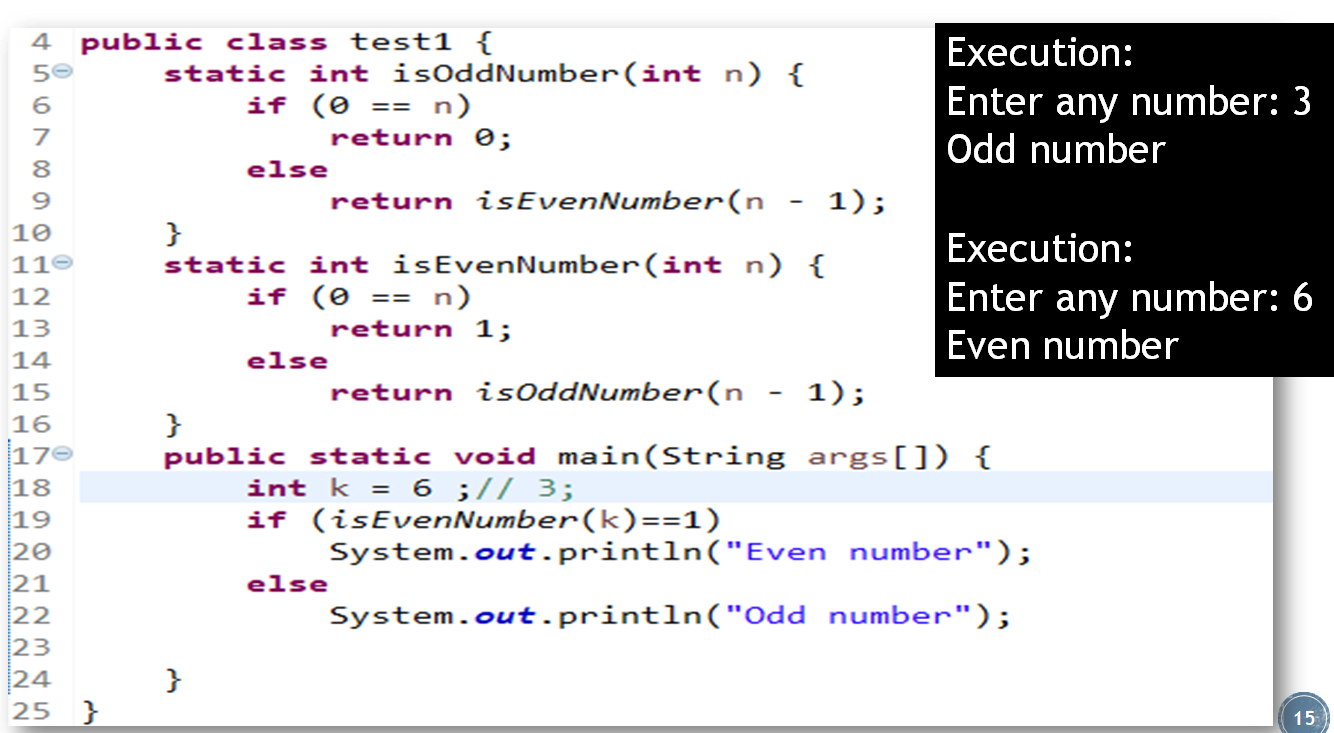
Calling two or more functions mutual is called mutual recursion. Say for example, if function A is calling B and function B is calling A recursively then it is said that, they are in mutual recursion.
Here in the following example isEvenNumber() is calling isOddNumber() and isOddNumber() is calling isEvenNumber()
相互调用两个或多个函数称为相互递归。 例如,如果函数A递归调用B而函数B递归调用A,则可以说它们是相互递归的。
在下面的示例中,isEvenNumber()调用isOddNumber(),isOddNumber()调用isEvenNumber()
Write an algorithm to find the factorial of a number entered by user.
编写算法以查找用户输入的数字的阶乘。
Step 1: Start
Step 2: Declare variables n,factorial and i.
Step 3: Initialize variables
factorial←1
i←1
Step 4: Read value of n
Step 5: Repeat the steps until i=n
5.1: factorial←factorial*i
5.2: i←i+1
Step 6: Display factorial
Step 7: Stop
Write an algorithm to find the largest among three different numbers entered by user.
编写一种算法,以查找用户输入的三个不同数字中的最大数字。
Step 1: Start
Step 2: Declare variables a,b and c. Step 3: Read variables a,b and c.
Step 4: If a>b
If a>c
Display a is the largest number.
Else
Display c is the largest number.
Else
If b>c
Display b is the largest number.
Else
Display c is the greatest number.
Step 5: Stop
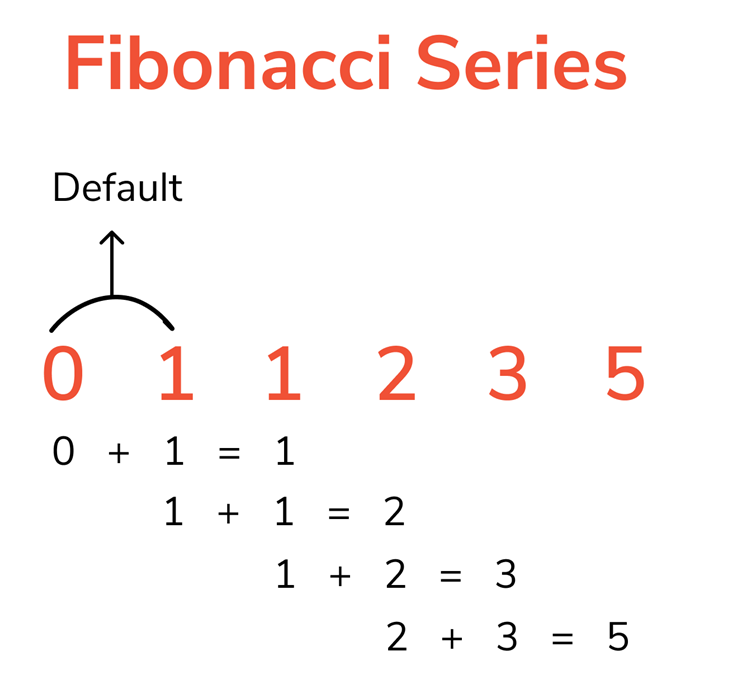
Write an algorithm to find the Fibonacci series till term≤100.
编写算法以找到直到项≤100的斐波那契数列。
Step 1: Start
Step 2: Declare variables first_term,second_term and temp.
Step 3: Initialize variables first_term←0 second_term←1 Step 4: Display first_term and second_term
Step 5: Repeat the steps until second_term≤1000
- temp←second_term
- second_term←second_term+first term
- first_term←temp
- Display second_term
Step 6: Stop
Step 1: Start
Step 2: Declare variables n,factorial and i.
Step 3: Initialize variables factorial←1
i←1
Step 4: Read value of n
Step 5: Repeat the steps until i=n
5.1: factorial←factorial*i
5.2: i←i+1
Step 6: Display factorial
Step 7: Stop
Step 1: Start
Step 2: Read number n
Step 3: Call factorial(n)
Step 4: Print factorial f
Step 5: Stop
factorial(n)
Step 1: If n==1 then return 1
Step 2: Else
f=n*factorial(n-1)
Step 3: Return f
Step 1: Start
Step 2: Declare variables first_term,second_term and temp.
Step 3: Initialize variables first_term←0 second_term←1
Step 4: Display first_term and second_term
Step 5: Repeat the steps until second_term≤n
- temp←second_term
- second_term←second_term+first term
- first_term←temp
- Display second_term
Step 6: Stop
Chapter4: Strack
A stack is a type of data structure that allows you access to a single element at any given time.
Stack is an ordered list in which, insertion and deletion can be performed only at one end that is called top.
Stack is a recursive data structure having pointer to its top element.
Stacks are sometimes called as Last-In-First-Out (LIFO) liss i.e. the element which is inserted first in the stack, will be deleted last from the stack.
Inserting an item is known as “pushing” onto the stack. “Popping”
off the stack is synonymous with removing an item.
堆栈是一种数据结构,可让您在任何给定时间访问单个元素。
堆栈是一个有序列表,其中只能在称为top的一端执行插入和删除操作。
堆栈是一种递归数据结构,具有指向其顶部元素的指针。
堆栈有时称为后进先出(LIFO)格式,即在堆栈中最先插入的元素将从堆栈中最后删除。
插入项目称为“推入”堆栈。 “流行”
堆叠是删除项目的代名词。
push() − Pushing (storing) an element on the stack.
pop() − Removing (accessing) an element from the stack.
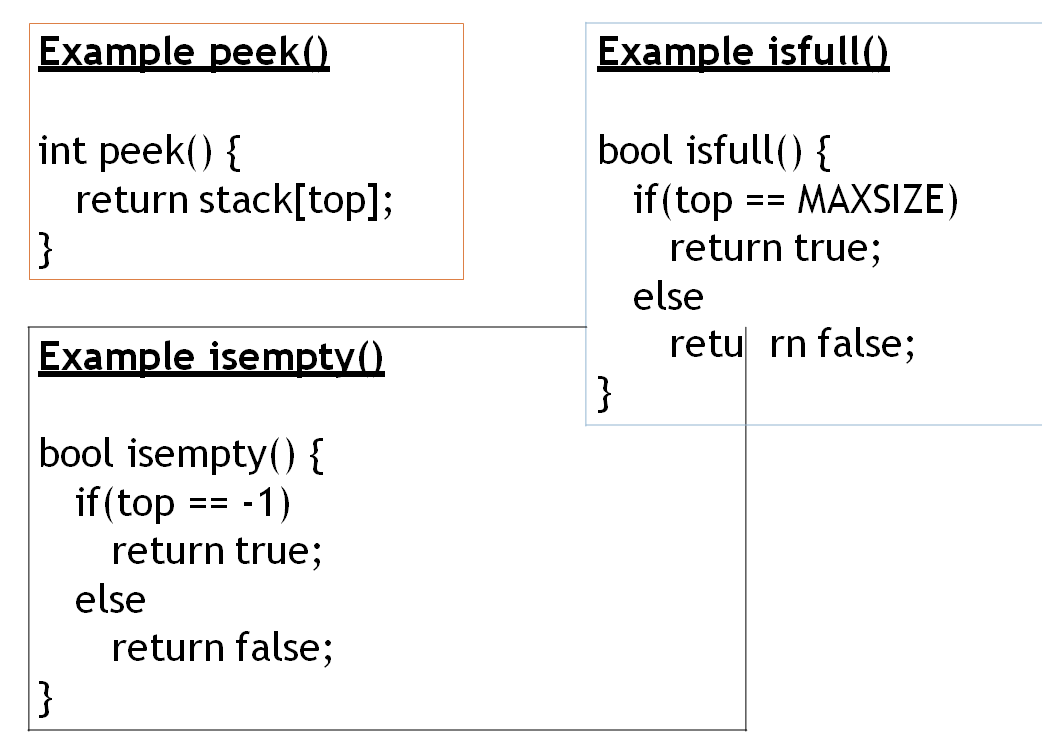
peek() − get the top data element of the stack, without removing it.
isFull() − check if stack is full.
isEmpty() − check if stack is empty.
push()-在堆栈中压入(存储)一个元素。
pop()-从堆栈中删除(访问)元素。
peek()-获取栈顶数据元素,不带删除它。
isFull()-检查堆栈是否已满。
isEmpty()-检查堆栈是否为空。
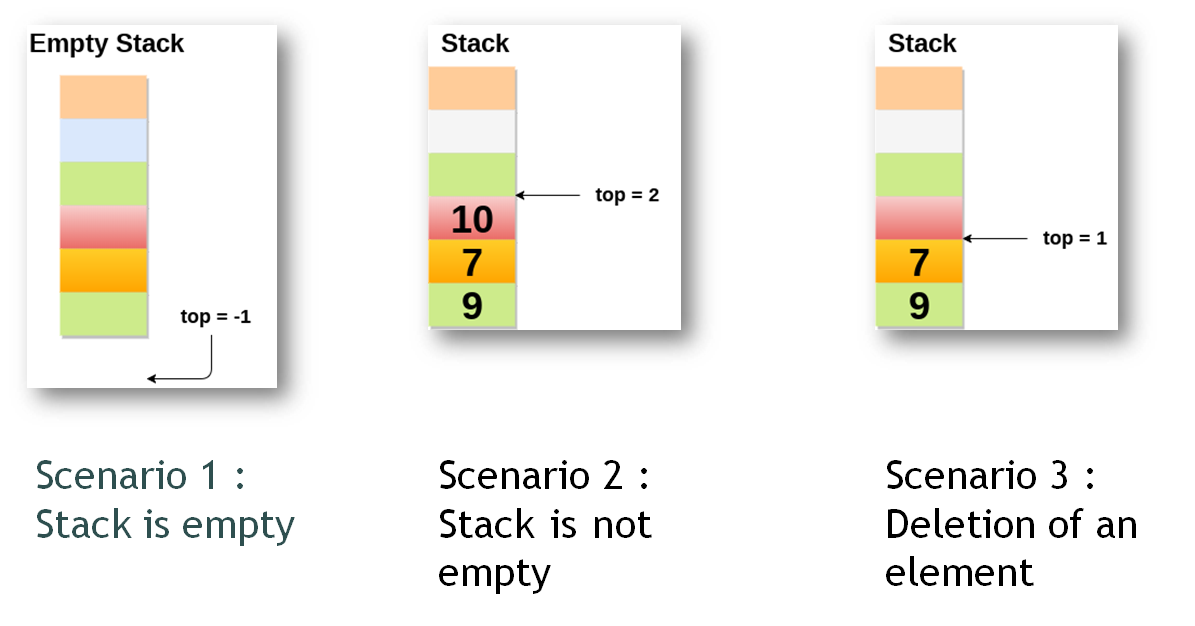
In the array implementation, we would:
- Declare an array of fixed size (which determines the maximum size of the stack).
- Keep a variable which always points to the “top” of the stack.
- Contains the array index of the “top” element.
在数组实现中,我们将:
- 声明一个固定大小的数组(它确定堆栈的最大大小)。
- 保留一个始终指向堆栈“顶部”的变量。
- 包含“ top”元素的数组索引。
The process of putting a new data element onto stack is known as a Push Operation. Push operation involves a series of steps −
Step 1 − Checks if the stack is full.
Step 2 − If the stack is full, produces an error and exit.
Step 3 − If the stack is not full, increments top to point next empty space.
Step 4 − Adds data element to the stack location, where top is
pointing.
Step 5 − Returns success.
将新数据元素放入堆栈的过程称为推入操作。 推送操作涉及一系列步骤-
步骤1-检查堆栈是否已满。
步骤2-如果堆栈已满,则产生错误并退出。
步骤3-如果堆栈未满,则从顶部开始递增以指向下一个空白空间。
步骤4-将数据元素添加到堆栈位置,顶部是
指向。
步骤5-返回成功。
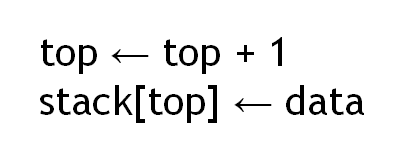
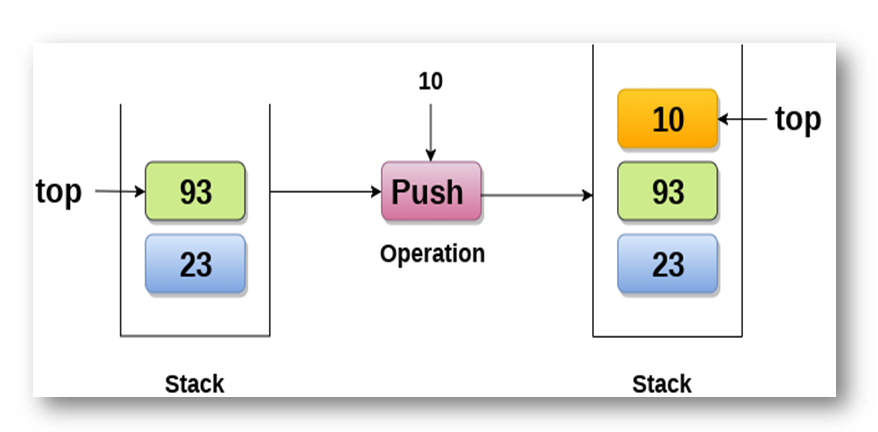
void push(int data) { if(!isFull()) {
top = top + 1; stack[top] = data;
} else {
system.out.println("Could not insert data, Stack is full.");
}
}
Accessing the content while removing it from the stack, is known as a Pop Operation. A Pop operation may involve the following steps −
Step 1 − Checks if the stack is empty.
Step 2 − If the stack is empty, produces an error and exit.
Step 3 − If the stack is not empty, accesses the data element at which top is pointing.
Step 4 − Decreases the value of top by 1.
Step 5 − Returns success.
在将内容从堆栈中删除的同时访问内容称为弹出操作。 弹出操作可能涉及以下步骤-
步骤1-检查堆栈是否为空。
步骤2-如果堆栈为空,则产生错误并退出。
步骤3-如果堆栈不为空,则访问顶部指向的数据元素。
步骤4-将top的值减小1。
步骤5-返回成功。

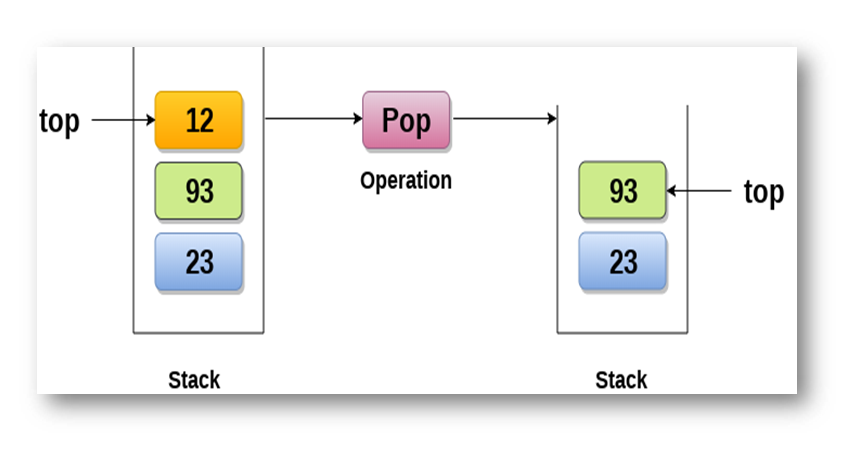
int pop() { if(!isempty()) {
int data = stack[top]; top = top - 1;
return data;
} else {
system.out.println("Could not retrieve data, Stack is empty.");
}
}
- Balancing symbols
- Postfix expressions
- Infix to postfix conversion
- Recursion
- 平衡符号
- 后缀表达式
- 中缀到后缀的转换
- 递归
Infix Notation
Prefix (Polish) Notation
Postfix (Reverse-Polish) Notation
中缀符号
前缀(波兰语)表示法
后缀(反向波兰语)表示法
We write expression in infix notation, e.g. a - b + c, where operators are used in-between operands.
It is easy for us humans to read, write, and speak in infix notation but the same does not go well with computing devices.
我们用中缀表示法来编写表达式,例如 a-b + c,其中在操作数之间使用运算符。
对于人类来说,以中缀符号进行阅读,书写和说话很容易,但是在计算设备上却不能很好地兼容。
In this notation, operator is prefixed to operands, i.e. operator is written ahead of operands.
For example, +ab.
This is equivalent to its infix notation a + b. Prefix notation is also known as Polish Notation.
在这种表示法中,运算符以操作数为前缀,即,运算符被写在操作数之前。
例如,+ ab。
这等效于其后缀符号a + b。 前缀表示法也称为波兰表示法。
This notation style is known as Reversed Polish Notation. In this notation style, the operator is postfixed to the operands i.e., the operator is written after the operands.
For example, ab+. This is equivalent to its infix notation a + b.
这个符号风格被称为逆波兰式。 在这种表示方式中,运算符后缀到操作数之后,即运算符写在操作数之后。
例如,ab +。 这等效于其后缀符号a + b。
The following table briefly tries to show the difference in all three notations

Following is algorithm for evaluation postfix expressions.
Create a stack to store operands (or values).
Scan the given expression and do following for every scanned element.
- If the element is a number, push it into the stack
- If the element is a operator, pop operands for the operator from stack. Evaluate the operator and push the result back to the stack
When the expression is ended, the number in the stack is the final answer
以下是评估后缀表达式的算法。
创建一个堆栈来存储操作数(或值)。
扫描给定的表达式,然后对每个扫描的元素执行以下操作。
-如果元素是数字,则将其推入堆栈
-如果元素是运算符,则从堆栈中弹出该运算符的操作数。 评估运算符并将结果推回堆栈
表达式结束时,堆栈中的数字是最终答案
For instance, the postfix expression 6 5 2 3 + 8 ∗ + 3 + ∗
The first four symbols are placed on the stack. The resulting stack is
例如,后缀表达式6 5 2 3 + 8 ∗ + 3 + ∗
前四个符号放置在堆栈上。 生成的堆栈是

Next a ‘+’ is read, so 3 and 2 are popped from the stack and their sum, 5, is pushed.
接下来读取一个“ +”,因此从堆栈中弹出3和2,并压入它们的总和5。
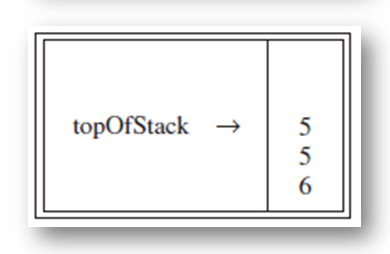
6 5 2 3 + 8 ∗ + 3 + ∗ Next 8 is pushed
6 5 2 3 + 8 ∗ + 3 + ∗下一个8被推动

Now a ‘∗’ is seen, so 8 and 5 are popped and 5 ∗ 8 = 40 is pushed.
现在看到一个“ ”,所以弹出8和5,并推5 8 = 40。

Next a ‘+’ is seen, so 40 and 5 are popped and 5 + 40 = 45 is pushed.
接下来看到一个“ +”,因此弹出40和5,并推入5 + 40 = 45。

Now, 3 is pushed.
现在,推3。

Next ‘+’ pops 3 and 45 and pushes 45 + 3 = 48.
下一个“ +”会弹出3和45,然后按45 + 3 = 48。

Finally, a ‘∗’ is seen and 48 and 6 are popped; the result, 6 ∗ 48 = 288, is pushed.
最后,看到一个“ ”,弹出48和6。 结果6 48 = 288。

example:
5 1 2 + 4 × + 3 −
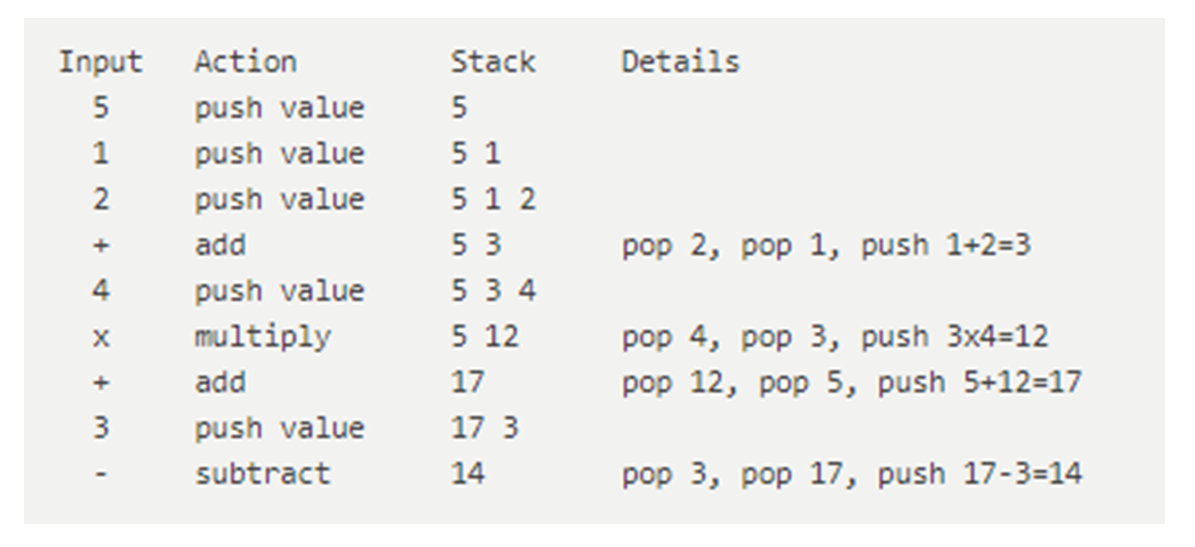
emmmm如果你要问我为啥会有这玩意
因为会考啊!
真的会考啊
别问我怎么知道的
在Postfix notation 前缀表示中,运算符会在数字之前
举个栗子的话就像 A + B -> AB+
同时这种变化我们也可以称作 Reverse Polish Notation
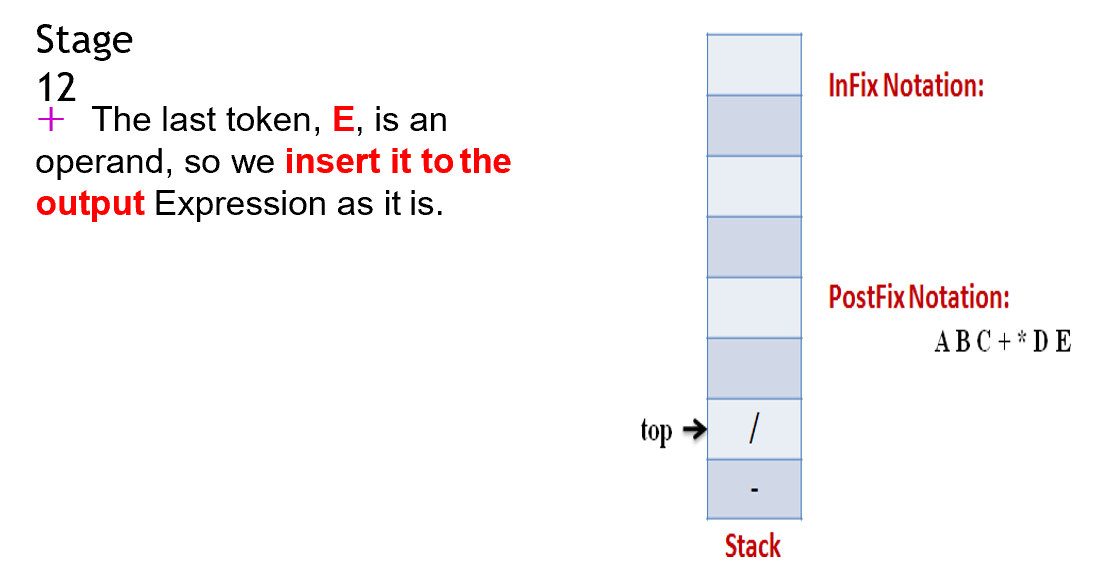
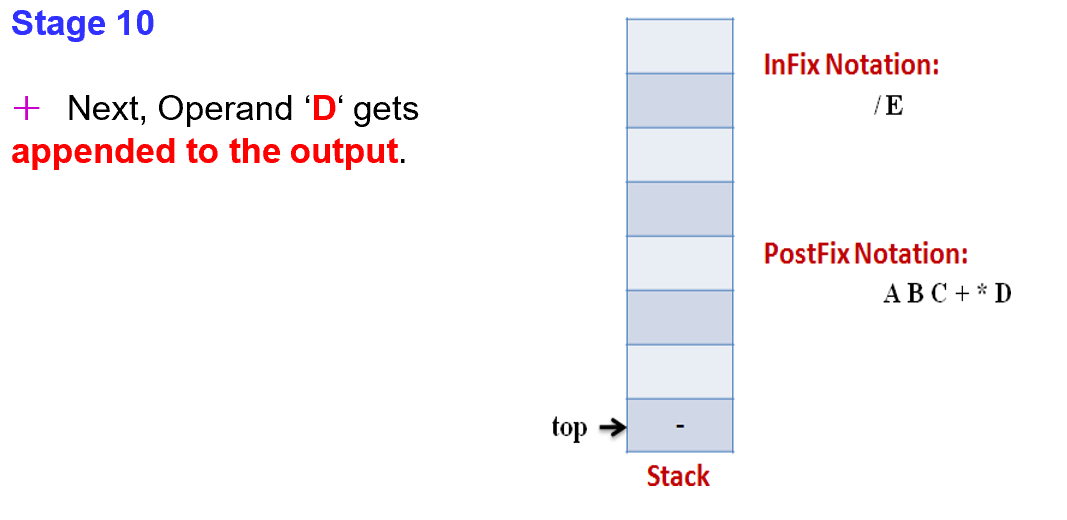
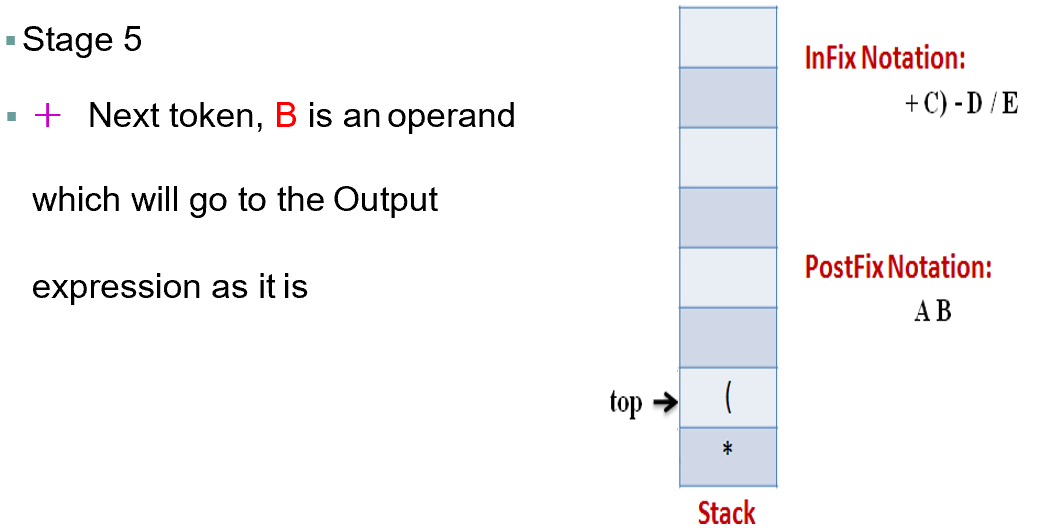
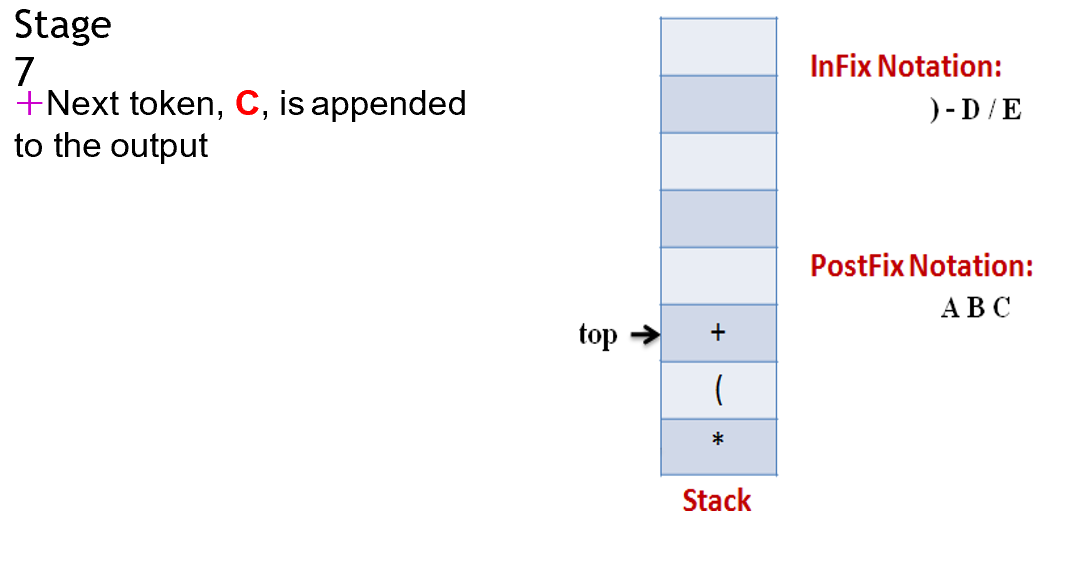
首先我们先来看看如何把简单的表达式强行变成我们看不懂的样子,也叫CONVERSION FROM INFIX TO POSTFIX ALGORITHM
Step 1:
Scan the Infix expression from left to right for tokens (Operators, Operands & Parentheses) and perform the steps 2 to 5 for each token in the Expression
Step2
If token is operand, Append it in postfix expression
如果是加减乘除符号的话,就把它丢到后面的运算符中
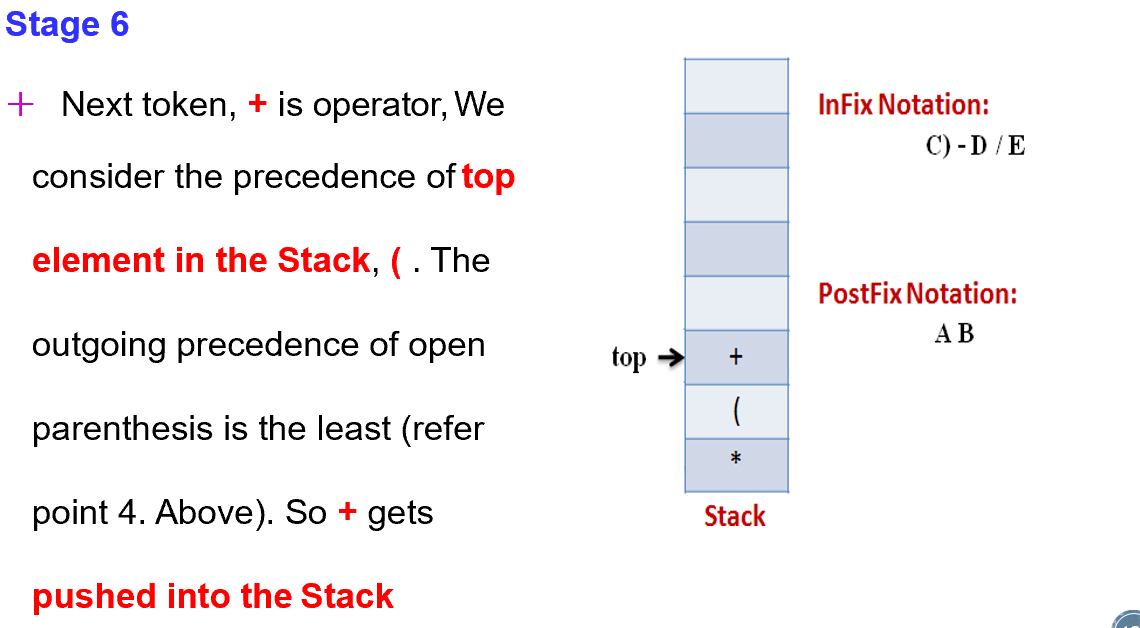
Step3
If token is a left parentheses “(“, push it in stack
Step4
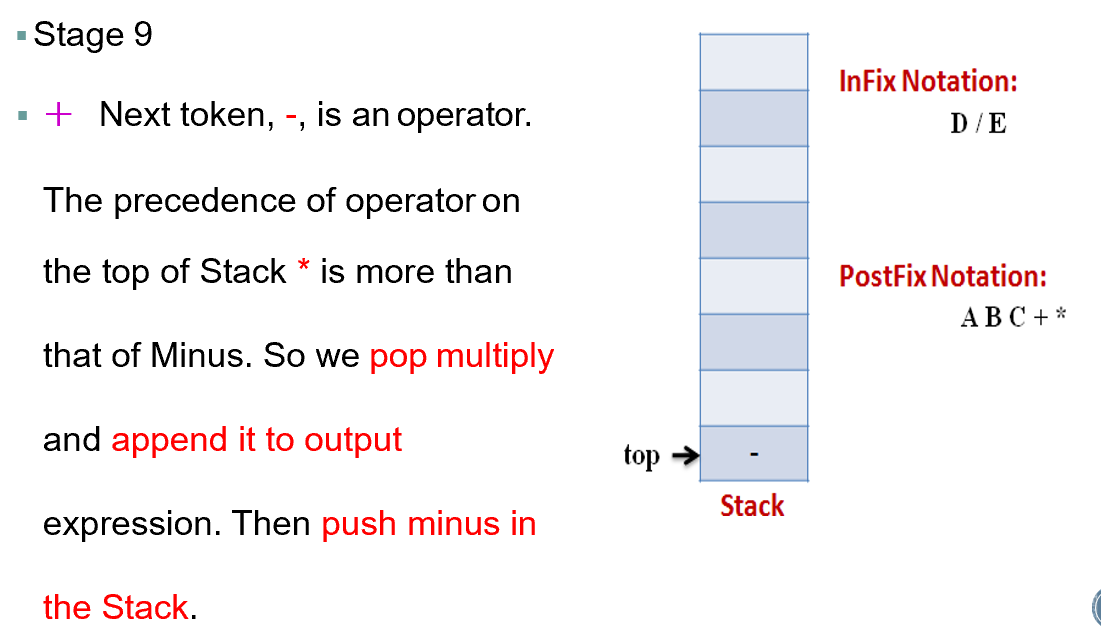
If token is an operator, Pop all the operators which are of higher or equal precedence then the incoming token and append them (in the same order) to the output Expression. After popping out all such operators, push the new token on stack.
Step5
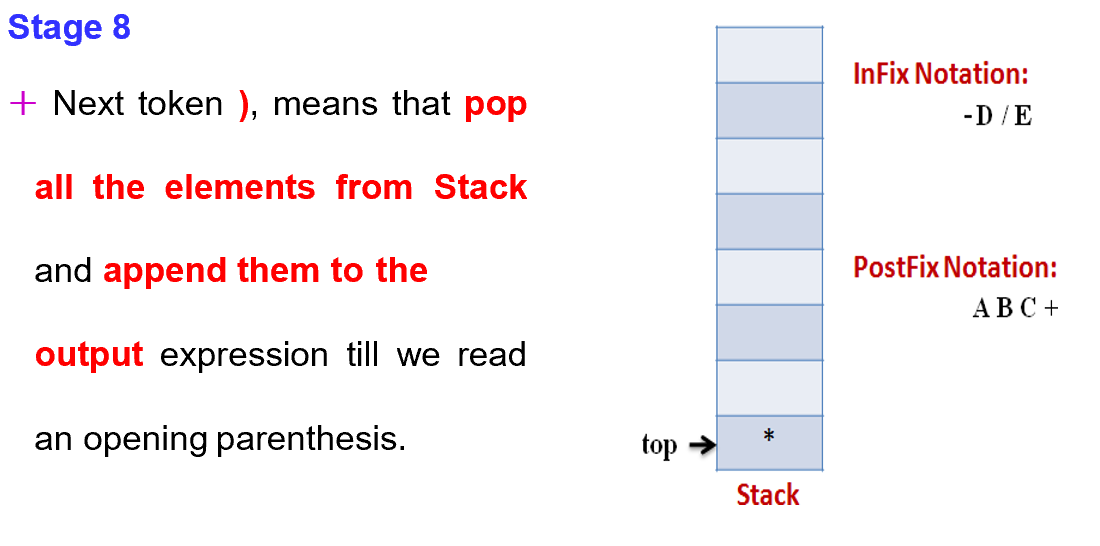
If “)” right parentheses is found, Pop all the operators from the Stack and append them to Output String, till you encounter the Opening Parenthesis “(“. Pop the left parenthesis but don’t append it to the output string (Postfix notation does not have brackets).
Step 6
When all tokens of Infix expression have been scanned. Pop all the elements from the stack and append them to the Output String. The Output string is the Corresponding Postfix Notation.
啊哈
不懂了吧
没错我看到上面这一坨玩意我也是挺绝望的
反正就是看不懂
那,来看个栗子吧
感觉还是用栗子比较好理解亿点点