首先!尤其感谢CC能给我课件拯救我的数据结构!!
我当然不能只看看而已
而是要真正的做好笔记!
就是这么认真的态度(叉腰)
now , show we begin
这里我们走!(here we go)
Chapter 1: Introduction
首先,不免有一个问题,啥是数据结构和算法 Data Structure and Algorithm (Java)
这种看起来很厉害的名字
其实真的挺厉害的(小声BB)
那我们先来看一个小例子,假如想要一个计算汽车多少公里耗油的小程序,那么就需要以下步骤:
Step 1: Declare a double variable named kilometers with initial value 10;
步骤1:声明一个初始值为10的双变量km;
Step 2: Declare a double constant named PRICE_PER_LITER with value 3.5;
步骤2:声明一个名为PRICE_PER_LITER的双常量,其值为3.5;
Step 3: Declare a double variable named total, multiply kilometers and PRICE_PER_LITER, and assign the result to total.
步骤3:声明一个名为total的双变量,将公里数和PRICE_PER_LITER相乘,然后将结果赋给total。
Step 4: Display total to the console.
步骤4:将总计显示到控制台。
你要问我上学期学的东西,啥是最难的话
那肯定是数组了
这玩意容易错还不说
还能玩出花来
那么,从数组中找到最大、最小的数字那就是数据结构最常干的事儿了
比如说:
(1) Create an array named myList with 10 double numbers which are inputted from the console.
(1)创建一个名为myList的数组,该数组具有从控制台输入的10个双数。
(2) Calculate the sum and average of the 10 double numbers. And then display the sum and average respectively.
(2)计算10个双数的和和平均值。 然后分别显示总和和平均值。
(3) Find the smallest number and its index. And then display the smallest number and its index respectively.
(3)找到最小的数字及其索引。 然后分别显示最小的数字及其索引。
那么话说回来,到底啥事数据结构呢?
Data is collection of facts and figures.
数据是事实和数字的集合。
Structure is the way of organizing so that easily readable.
结构是使组织易于阅读的方式。
我们可以给这个下一个定义:
“Data structure is a form or organizing of data into structurally defined format which may be readable or when ever it is required it may retrieve”.
“数据结构是一种数据形式或组织,可以是可读的或在需要时可以检索的结构定义的格式”。
An algorithm is a procedure or formula for solving a problem, based on conducting a sequence of specified actions.
算法是基于执行一系列指定动作来解决问题的过程或公式。
那么我们可以将其总结为:程序 = 算法 + 数据结构
算法的核心是创建问题抽象的模型和明确求解目标
我们之所以学习数据结构,是为了更好的收集和处理数据。数据结构是数据按照某种方式或者顺序来排列,这样我们可以更加快速地查找和储存数据。在java之中,我们学习了8种原始数据类型,我们可以使用他们来处理一些数据。
同时,数据的设计应该实现降低复杂性和提高效率这两个目标
一般的,数据数据结构需要满足几个指标:正确性、时间复杂度、空间复杂度
正确性:应该准确无误
时间复杂度:用时越短越好
空间复杂度:占用内存越少越好
which one of the follow opions is a kind of reference data type?
A. int
B. float
C. String
D. char
答案是C!String!
referencr data type 引用数据类型
primitive data type 原始数据类型
你知道这两个玩意有什么区别吗?
我们在上学期学过8大原始数据类型
你别告诉我你忘掉了
忘了原始数据类型自觉去背!
int float byte double char boolean short long
然后引用数据类型就是除了这8种原始数据类型之外的所有数据类型啦
无论是java自带的还是我们自己定义的全都算数!
什么?你说这玩意太简单了上学期学过不想再看了????
那来看看 Abstract Data Type (ADT) 抽象数据类型吧
咳咳,为啥要同时讲3种数据类型?当然是为了让你混乱啦
哈哈哈哈
毕竟从入门到放弃才是java的精华
具体你要给抽象数据类型下一个定义的话
好像也太难了
还是看几个例子吧
Linked List 链表
Tree 树
Graph 图
Stack 栈
Queue 队列
你看在上面的这些例子中,基本上全都是已经包装好了的方法,我们只需要直接拿来用就可以了
也就是说,当我们最开始定义一个大项目的时候,需要想象这个项目能够实现哪些功能,然后将这些实现功能的方法封装起来,后期只需要按照规定的接口直接调用就可以了,并不需要知道这个方法到底是怎么实现的(也不想知道),这个就叫做抽象的方法
那么抽象数据类型也是类似的,我们就是将数据对象和对象之间的关系封装在一起,到后面直接用就可以了
然后你要是还不清楚的话,那还是不要搞清楚比较好
毕竟记太多的定义也是挺麻烦的
常见的线性结构有: 一维数组 array 、队列 quene 、栈 strack、多维数组 Multi-dimensional array
常见的非线性结构有: 树 tree、图 garph
在生活中,我们也能看到许多线性结构的例子
比如排成一行的队伍,每一个人都有一个与之对应的名次
比如你是第一个我是第二个之类的
又比如一摞饼干,也是一个简单的队列
对于非线性结构,就是一个元素可能与多个元素对应
比如常见的树图
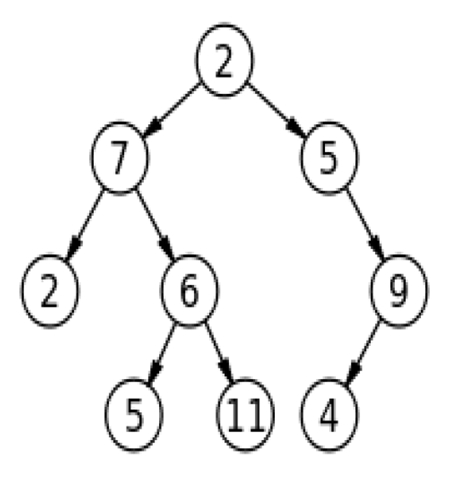
什么?你说这玩意长的不想一个大树???
那倒过来看呢
像了吧~
反正只要元素不是一一对应的话,都可以称之为非线性结构
就像城市之间的高速公路
不同的高速公路将多个城市串起来
并且城市之间互相都有公路能到达其他城市
这个就是 图
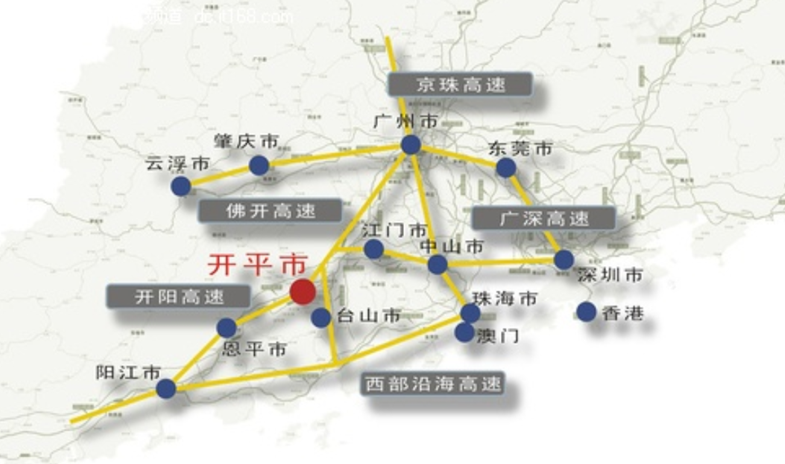
这个其实很好理解,字面意思罢了
不过还是用图片举个栗子比较好理解一点

那么,有人可能要问了,这么多种不同种类的结构,到底有什么用呢当然是用来考试了
(笑)
至于选取哪个结构,取决于不同的问题种类和类型
所谓的因地制宜说的大概也就是这样子吧
诶对了,不知道你还记不记得这门科目的名字
“数据结构与算法”
对的,接下来就是算法的问题
算法一般都用于数据处理、计算和其他相关的数学运算问题,也可以用于操作数据。比如插入新数据项,搜索特定项或对项进行排序
注:算法并不是一套完整的代码或者程序,它只是问题的核心逻辑步骤,或者你可以叫它问题的解决方案
我们可以将其表示为 pseudocode 伪代码 或 flowchart 流程图
那我们来举个栗子吧
首先登场的是 pseudocode 伪代码
这玩意并不是标准的代码语言,它类似于代码的模块化结构,但是使用英语的语法,能让noob程序员快速理解代码的含义和意思

其次是flowchart 流程图
这个我就不多BB了
当年被RT说的,流程图真的很重要,特别是大型的项目
不然代码逻辑跟蜘蛛网似的
一般来说,算法都具有以下性质:
输入 Input
该算法应从外部提供0个或多个输入。
输出 Output
至少应获得1个输出。
确定性 Definiteness
算法的每一步都应该清晰明确。
正确性 Correctness
算法的每一步都必须产生正确的输出。
有限度 Finiteness
该算法应具有有限数量的步骤。
那么,这里有个小例题:
A: input and output
A: pseudocode and flowchart
说起来,你知道算法的本质是啥嘛
数学啊
既然是数学,那肯定少不了一个玩意
是的没错
就是f(x) 数学公式了
一般来说,我们熟悉的数学函数都可以用一个“简单的”公式描述
比如
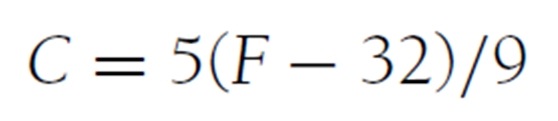
你看上面那个公式,如果我说要用它写一个java小程序
你肯定会说:就这?
嗯
嗯哼?
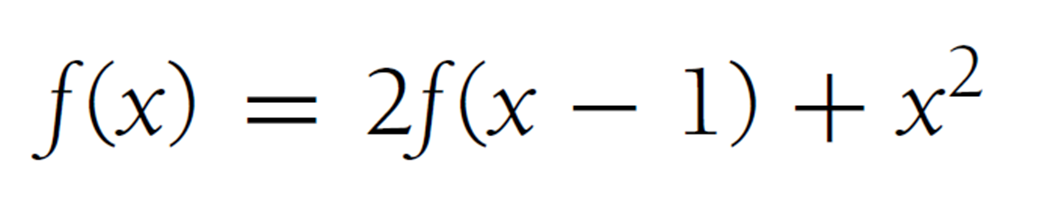
嗯?怎么样不会了吧
你看给函数套个娃,难度就成几何倍数上涨
但是为了应付这玩意,我们也有对应的东西来对抗它
我们把这个玩意称之为 recursive 递归
让我们看到上面的那个图片中的秘制公式
如果将其写为java程序的话,那多半是

可以看到,我们是将其中套了一个 终止条件 base case
简单来说,终止条件就是递推中最底层的最基本的一个操作,当程序走到这一步递归就不会再无线走下去
那你有没有想过,为啥这玩意叫递归呢?
首先我们参考上面的栗子,想一下下面这个方程应该怎么用程序表达出来
F(n) = n * F(n – 1), F(1) = 1
比如说设定 n = 6,那思路应为:

可以看到,因为其中含有函数本身,所以起本质为一个套娃
我们可以将这个理解为递归中的“递”

然后我们知道,f(1) = 1, 那么就可以反推该函数公式得到:

然后这个,就是递归之中的“归”了


嗯如果你要说这函数是我们自己捏造的没啥意思
那我们来看看斐波那契数列 Fibonacci sequence 吧
嗯我知道你肯定不懂啥是斐波那契额数列
那我给你举个栗子
假如一对大兔子能够繁殖一只大兔子和一只小兔子
小兔子可以长成大兔子然后继续繁衍
那么从最开始的1对兔子时候开始,每一回合(每一行)的兔子的数量是多少呢?
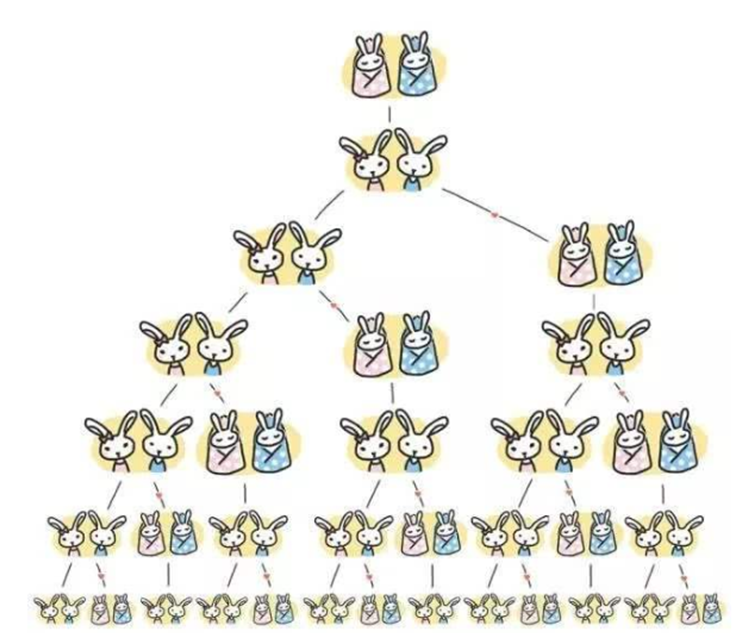
不难发现,从上往下的兔子的对数应该是1、1、2、3、5、8、13、21、34….
诶,你说这个数字意味着什么
意味着猫

啊不好意思放错了
嗯就是知道怎么去理解就好啦
重头戏是如何用java去表达

那么,我们不难总结出递归的基本法则:
2、在递归中,必须朝着取得进展 Making progress 的方向前进
3、所有的递归调用都有效并且符合设计规则 Design rule
4、合成效益法则 compound interest rule 同一个实例不能做重复的工作
Chapter 2: Algorithm Analysis
接下来,我们来看看算法分析 algorithm analysis
之前提到,算法是一组用于解决问题的简单指令,但是我们在分析算法的时候,可以比较他们的 相对增长率 relative rates of growth
对于这玩意的表达方式,我们可以用 Big-O notation 大O表示法
是的没错!这玩意肯定得计算的啦
至于要算什么,那当然是函数复杂度啦 Complexity functions
函数复杂度是根据输入数据的数量 求出 算法 的时间复杂度和空间复杂度的方差
嗯我也乱的不行
那我们先来看看这些名词
time-complexity 时间复杂度 是指算法需要多长时间才能完成
space-complexity 空间复杂度 是指算法执行时的内存占用量
举个栗子

你看上面的O(1)只需要一步就能解决,
但是O(N)就需要16步才能解决
同样的,O ^ N 就需要256步(或者更多)才能解决,
综上所述,我们可以将大 O 标记法概括为:如果我们需要解决一定基数的问题,在不同的时间复杂度的情况下,每种算法需要运行的步数(例如循环次数)的一个比较情况

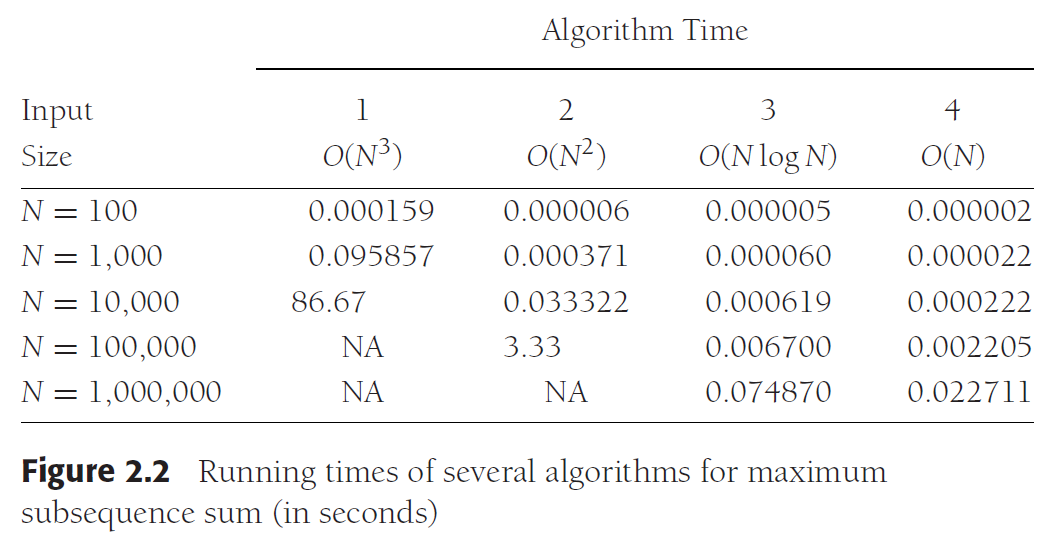
emmmm如果你不喜欢看这种干巴巴的数据的话
还可以来看看图
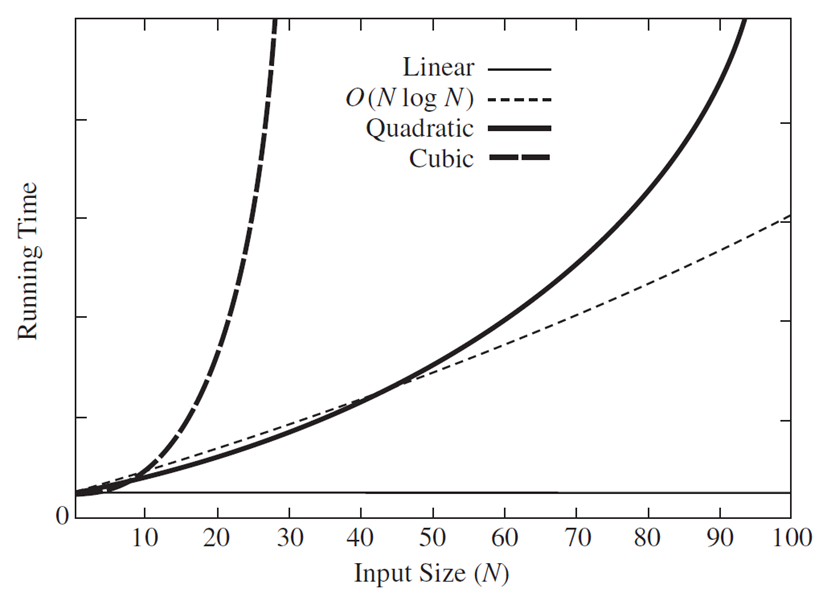
但是当我们放大N的值,就可以很明显地看出不同算法对所需要花费的时间的影响
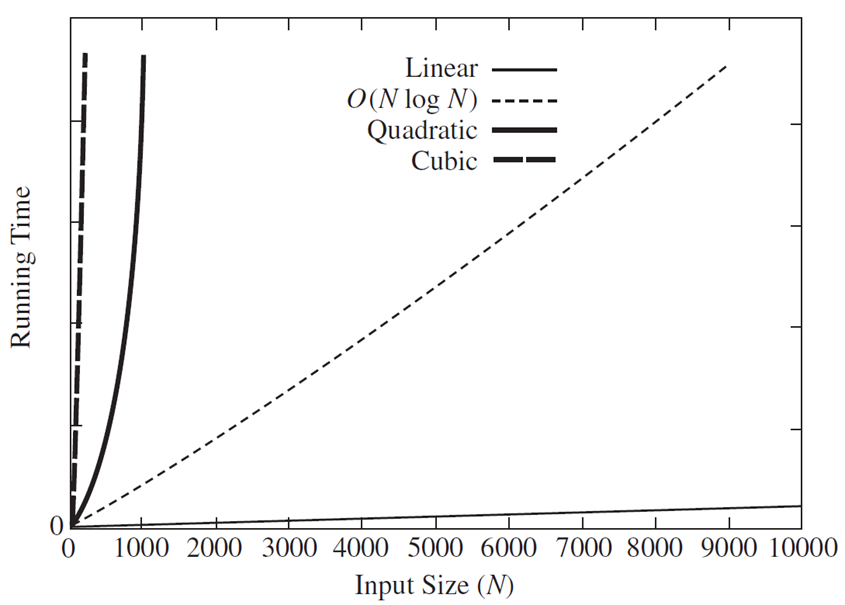
从上面的两张图中可以很容易地看出不同的算法对N值的影响是十分显著的
那么有没有一个专业的数值来描述这种东西呢?
巧了,还真有
无论你想不想看他都会来
并且考试还会考啊!!!
(:з」∠)
假如,我们需要计算一个i的N次方的函数,那我们不难写一个java程序

从上面这个例子可以联想到,当N的值越大的时候,函数所需要的内存和时间越多
那么,再联系几个小例子

假如我们分析一个算法得到的花销时间是一个数学表达式,但是在这个表达式之中,只有最高次幂的部分对整个时间花销影响最大
所以大O表示法也只会保留最高次幂的部分,而直接忽略低次幂的部分,同时系数也不会保留

就拿上面的那个例子来说,你看5 * n ^ 2 这个例子,这个式子里面N的平方才是对整个运行时间影响最大的
那么,现在,该谈谈结论了
一般我们有4种循环语句,每一种都有不同的表达方式
for循环运行时间的最大值为 for循环语句内的运行时间 * 迭代次数(说白了就是循环了多少次)
Nested Loops
一组嵌套循环中的 Base case 的运行时间是 Base case的运行时间 * 所有循环的大小
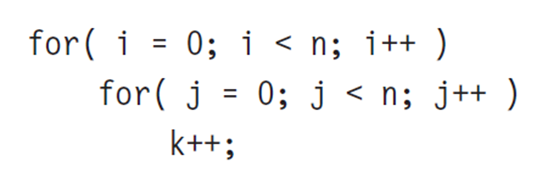
Consecutive Statements
其实也就是两个连起来的函数罢了,复杂度就是两个函数相加
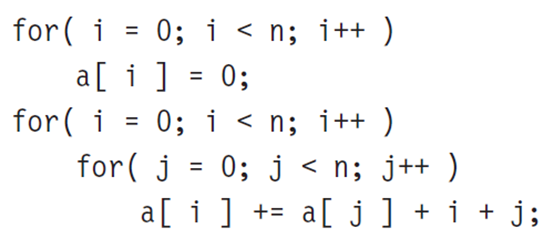
你看上面这个栗子来说,其实就是计算N的平方
因为用两个for循环,来表示n * n这样一个意思
那么可以得出,这个的复杂度应为:O(N) + O(N ^2 )
因为前面的一次幂根本不重要,所以我们只需要把重点放在二次幂上面就好了
所以最终的空间复杂度应为: O (N ^ 2)
if/else
运行时间永远不会比运行两个的时间相加起来大

比如在这里的就是总的运行时间肯定小于 S1 和 S2 的运行时间之和
接下来 来看看算法所需要的空间吧
算法所需要的空间一般由一般由以下两个部分组成
固定的部分:储存数据和变量的空间。 这个与问题的大小无关。 比如,简单的变量和常量,程序的大小都会影响固定部分的大小
可变的部分:可变部分的大小取决于动态的内存分配、递归栈的空间等
哦对了,你知道不同的数据类型使用的内存是不一样的嘛
咱们来看一张图

如果算法执行所需要的临时空间不随着某个变量n的大小而变化,即此算法空间复杂度为一个常量,可表示为 O(1)

让我们先看一段代码

可以看到,这段代码中,第一行new了一个数组出来,这个数据占用的大小为n,这段代码的2-6行,虽然有循环,但没有再分配新的空间,因此,这段代码的空间复杂度主要看第一行即可,即 S(N) = O(N)
Chapter 3: Lists, Stacks, and Queues
首先,让我们回到 Abstract Data Type (ADTs) 抽象数据类型
在前面提到过,所谓的抽象数据类型其实就是一种特定操作,抽象的数据类型就是emmmmm
我还是不下定义比较好,反正也不考
比如 list, seats and graphs 都可以被所作为抽象的数据类型
举个栗子,当我们在玩游戏的时候(比如超级马里奥),我们就会对游戏内的人物进行一系列的操作

比如我们会给马里奥定义一系列的操作,比如前进。后退、跳跃、白给之类的操作,那么这个时候马里奥就是一个抽象数据类型。当我们定义了一个数据对象,对象中各个元素之间的关系 以及 对数据元素进行的操作 ,抽象数据类型体现了程序设计中问题的分解和信息隐藏的特征
如果在代码中实现的话大概就是这样子


首先,让我们来看 List ADT 列表抽象数据类型
让我们从一个小例子来了解
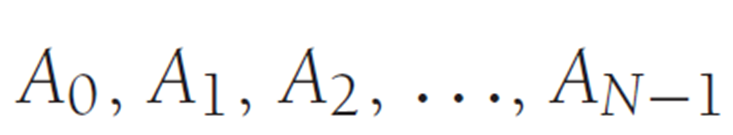
不难看出,列表的大小为 N
那么,我们可以将 N=0 的列表称之为 空列表 empty list
在上图中, 我们说 Ai 跟随 follows (或者叫 Successor 后继 Ai-1(i <N)
而Ai−1 (i < N) 也就是 Ai−1 precedes 前驱 Ai (i > 0)
元素Ai 在列表中的位置是 i
那么,在列表中,我们有一系列相关的最基本的操作
分别为 :
- printList
- makeEmpty
- find
- insert
- remove
- 等等等等
所有的这些相关操作都可以通过数组来实现。在前面我们提到过,创建数组的时候需要定义数组的大小,也就是数组有着 固定的容量fixed capacity 。所以我们可以在创建数组的时候可以创建容量翻倍的数组,以确保数组位置足够
然而,当我们往数组中加元素的时候,往往需要花费更多的时间。因为需要将增加之后的每一位都向后移动,也就意味着需要一个循环将所有的元素全部移动一次,最坏的情况下,可能出现 O(n)的情况
那不妨来看一个例题

A. This is an list to store integer numbers. 列表中储存着数字
B. The size of this list is 4. 列表大小为4
C. This list has a fixed capacity. 这个列表有固定的容量
答案: C

“are” 应在列表的 __
“morning” 应在列表的 _
“you” 应在列表的 __
A: 4 2 5
这里注意是多少位,千万不要搞混了
不是index啊啊啊啊啊
A. O(1)
B. O(N)
C. O(N^2)
D. O(N^3)
A: A
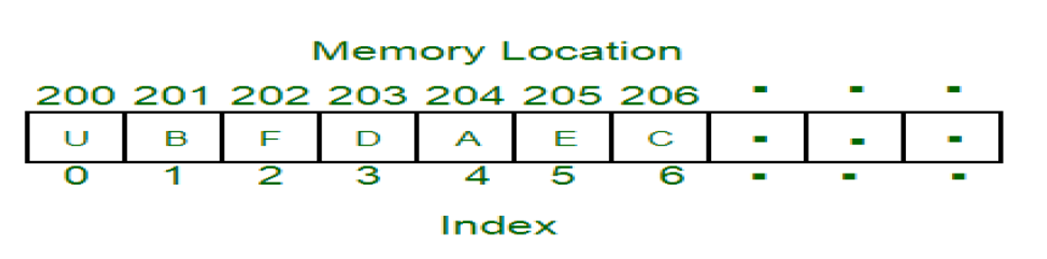
假如我们有N个数据,我们需要计算的是找到第一个数据,就只是需要根据数组下标,因为这个数组下标也对应了它在内存中的位置,所以就能很快速地定位到,所以这里的就是O(1),这个复杂度属于常量型复杂度(数组下标对应了在内存中的位置)
A. O(1)
B. O(N)
C. O(N^2)
D. O(N^3)
A: B
假如我们有N + 1个数据,我们需要计算的是删除第一个数据。假如删除元素之后还有N个元素,那么后面的N个元素全部都要往前面移动,这种情况就取决于N, 那么时间复杂度应为 O(N)
你看上面那个例题,为了删除数列中的其中一个项目,就得把整个数列全部都重新排列一遍,这个看起来真的超级麻烦
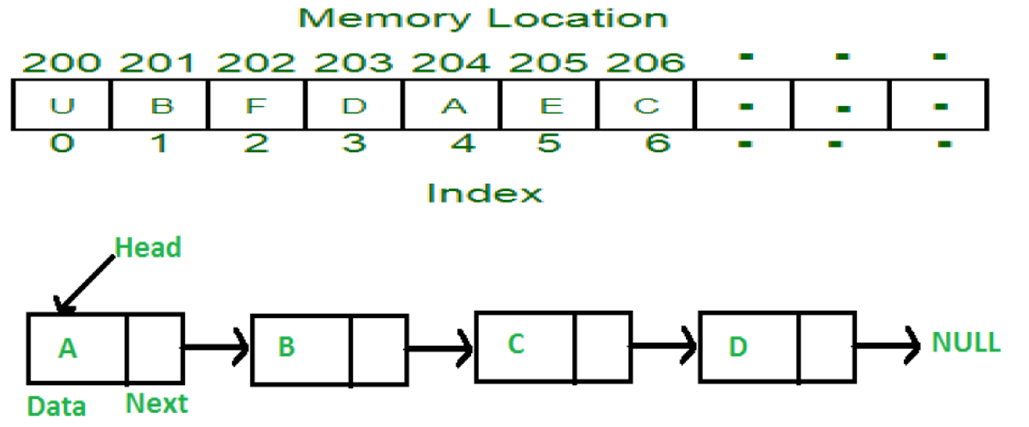
那么,我们不妨设计一下,假设这些用于储存的列表都是不相邻的,也就是说每一个都可以是独立的存在,我们没必要将他们按照顺序排列起来,他们之间只要有一定的顺序关系就可以了,比如我们可以用一系列的 节点 Node 表示,这些节点在内存中不一定相邻

可以看到,每一个节点都包含着这个 元素 element 以及 Successor 后继 元素的链接,但是最后有一个有点像电学接地的符号,这个我们将其叫做 null , 意思是我们可以我们随时留着一个位置,留给新加入的元素,或者其他可能会用到的元素。
举个栗子,如果我们需要printList 或者 find(x) 这一类的操作,那我们只需要将其一个接一个地打印出来就可以了,感觉也是挺不错哒,因为这个是 linear-time 线性时间
那么,关于删除和加入的操作,emmmmm......
one picture more than thoudsand word
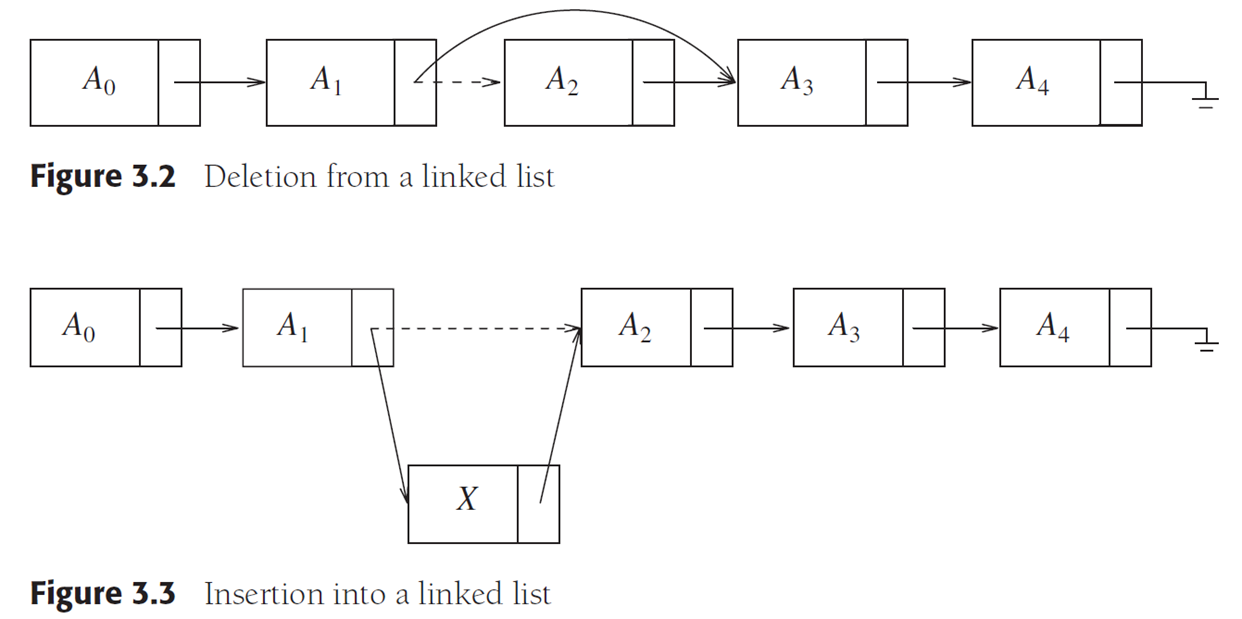
得了,上面这个图,dddd
相信你一定能看懂的
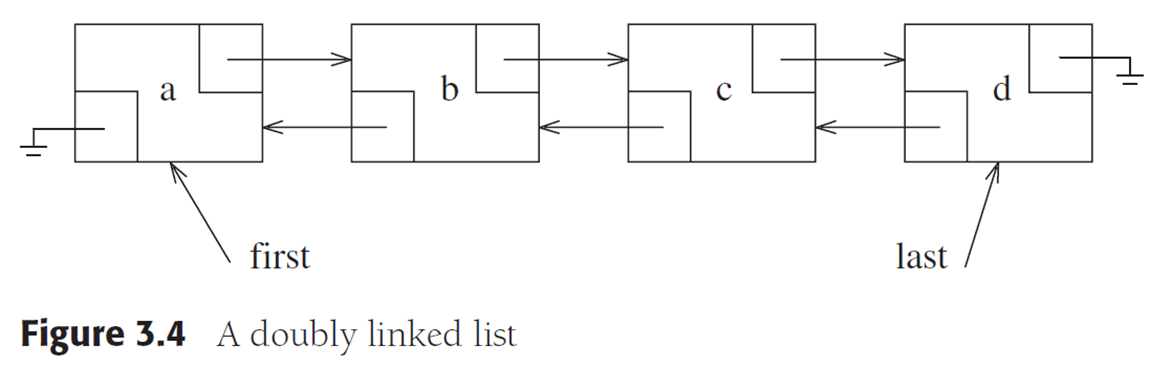
你看这个,就是双链表
它有两个指针,分别指向后继和前驱,所以双向链表可以很方便地从任意一个结点访问它的前驱和后驱结点
我感觉这玩意可以说是一个数学模型吧......
反正感觉这个肯定是一个基础
以后肯定有大用处
The Collections API resides in package java.util.
Collections 是一个包装类。它包含有各种有关集合操作的静态多态方法。此类不能实例化,就像一个工具类,服务于Java的Collection框架。The notion of a collection, which stores a collection of identically
typed objects, is abstracted in the Collection interface.
Collection 是一个集合接口。它提供了对集合对象进行基本操作的通用接口方法。Collection接口在Java 类库中有很多具体的实现。Collection接口的意义是为各种具体的集合提供了最大化的统一操作方式。
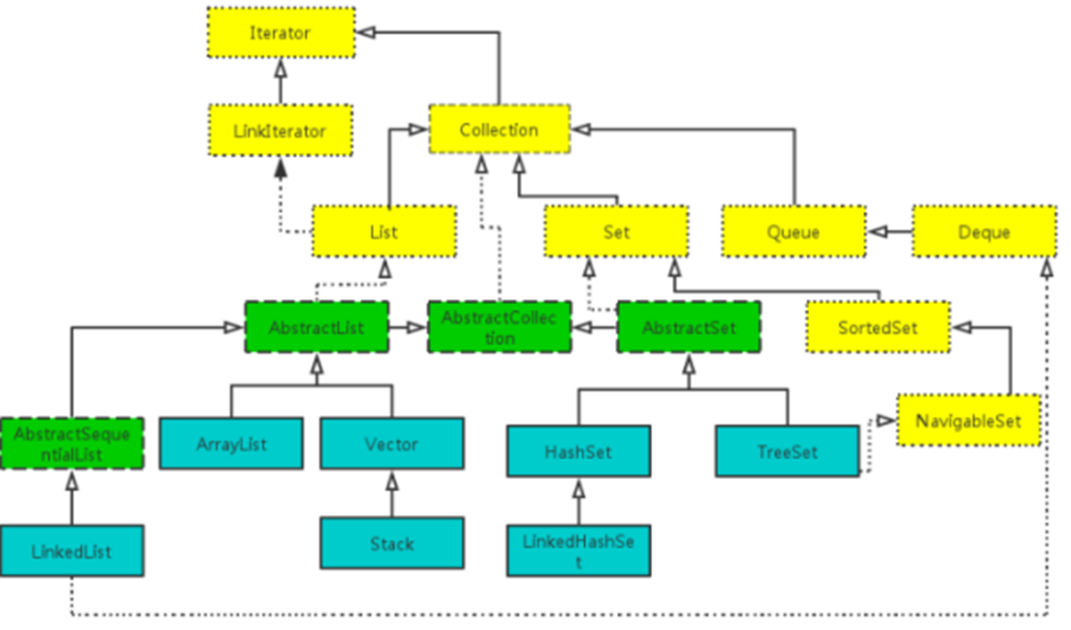
嗯,是的木有错,我也看傻了
果然太过于书面化的词语只能让人越看越傻
还是这样子说把
Collection其实只是是最基本的集合接口,一个Collection代表一组Object,即Collection的元素(Elements)。
一些Collection允许相同的元素,而另一些不行。一些能排序而另一些不行。Java SDK不提供直接继承自Collection的类,Java SDK提供的类都是继承自Collection的“子接口”,如List和Set。

假如我们已经通过自定义实现了interator接口,那么这个类的对象就可以使用for-each来遍历,否则是没办法使用for-each的

List 接口拓展了Collection,所以Collection包含接口中的所有方法,也包括其他的一些方法

ArrayList提供了一个 可拓展的数组 growable array , 缺点是除非是在数列末尾的null中加入新元素,否则如果在数列中间加入或者删除的话会消耗较大的资源(比如运算资源、时间等)
关于LinkedList的优点,只需要知道需要改变的位置,就可以方便的 插入 insertion 和删除现有的元素。但是缺点是LinkedList难以 索引 indexable , 除非我们需要的元素距离列表两端很近,否则就需要花费很大的资源去调用
比如,在LinkedList中,我们有addFirst和removeFirst,addLast和removeLast以及getFirst和getLast,以有效地添加,删除和访问列表两端的元素。
好啦好啦,言归正传,那么我们如何创建一个链表呢?
我们不妨先来看一个基本创建Linked List的方法
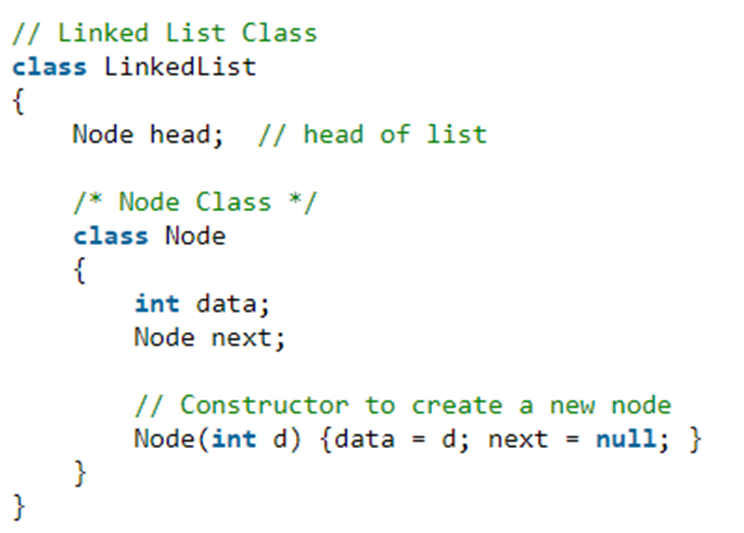
引用来源:https://blog.csdn.net/u010648555/article/details/58680439
java.lang.Object java.util.AbstractCollection<E> java.util.AbstractList<E> java.util.AbstractSequentialList<E> java.util.LinkedList<E> Type Parameters: E - the type of elements held in this collection All Implemented Interfaces: Serializable, Cloneable, Iterable<E>, Collection<E>, Deque<E>, List<E>, Queue<E>
boolean add(E e)
将指定元素添加到此列表的结尾。
void add(int index, E element)
在此列表中指定的位置插入指定的元素。
boolean addAll(Collection<? extends E> c)
添加指定 collection 中的所有元素到此列表的结尾,顺序是指定 collection 的迭代器返回这些元素的顺序。
boolean addAll(int index, Collection<? extends E> c)
将指定 collection 中的所有元素从指定位置开始插入此列表。
void addFirst(E e)
将指定元素插入此列表的开头。
void addLast(E e)
将指定元素添加到此列表的结尾。
void clear()
从此列表中移除所有元素。
Object clone()
返回此 LinkedList 的浅表副本。
boolean contains(Object o)
如果此列表包含指定元素,则返回 true。
Iterator<E> descendingIterator()
返回以逆向顺序在此双端队列的元素上进行迭代的迭代器。
E element()
获取但不移除此列表的头(第一个元素)。
E get(int index)
返回此列表中指定位置处的元素。
E getFirst()
返回此列表的第一个元素。
E getLast()
返回此列表的最后一个元素。
int indexOf(Object o)
返回此列表中首次出现的指定元素的索引,如果此列表中不包含该元素,则返回 -1。
int lastIndexOf(Object o)
返回此列表中最后出现的指定元素的索引,如果此列表中不包含该元素,则返回 -1。
ListIterator<E> listIterator(int index)
返回此列表中的元素的列表迭代器(按适当顺序),从列表中指定位置开始。
boolean offer(E e)
将指定元素添加到此列表的末尾(最后一个元素)。
boolean offerFirst(E e)
在此列表的开头插入指定的元素。
boolean offerLast(E e)
在此列表末尾插入指定的元素。
E peek()
获取但不移除此列表的头(第一个元素)。
E peekFirst()
获取但不移除此列表的第一个元素;如果此列表为空,则返回 null。
E peekLast()
获取但不移除此列表的最后一个元素;如果此列表为空,则返回 null。
E poll()
获取并移除此列表的头(第一个元素)
E pollFirst()
获取并移除此列表的第一个元素;如果此列表为空,则返回 null。
E pollLast()
获取并移除此列表的最后一个元素;如果此列表为空,则返回 null。
E pop()
从此列表所表示的堆栈处弹出一个元素。
void push(E e)
将元素推入此列表所表示的堆栈。
E remove()
获取并移除此列表的头(第一个元素)。
E remove(int index)
移除此列表中指定位置处的元素。
boolean remove(Object o)
从此列表中移除首次出现的指定元素(如果存在)。
E removeFirst()
移除并返回此列表的第一个元素。
boolean removeFirstOccurrence(Object o)
从此列表中移除第一次出现的指定元素(从头部到尾部遍历列表时)。
E removeLast()
移除并返回此列表的最后一个元素。
boolean removeLastOccurrence(Object o)
从此列表中移除最后一次出现的指定元素(从头部到尾部遍历列表时)。
E set(int index, E element)
将此列表中指定位置的元素替换为指定的元素。
int size()
返回此列表的元素数。
Object[] toArray()
返回以适当顺序(从第一个元素到最后一个元素)包含此列表中所有元素的数组。
<T> T[] toArray(T[] a)
返回以适当顺序(从第一个元素到最后一个元素)包含此列表中所有元素的数组;返回数组的运行时类型为指定数组的类型。
其实说了这么多,你也可以很明显地看到,LinkedList是Java中已经写好了的一个方法,我们可以直接拿来用的一个方法
一般我们也用不到什么高级的操作,但是关于最基本的东西还是要清楚的
比如看一下下面这张图

你看, java.util.LinkedList是不是包含在Object包里面吖
同时,LinkedList也是继承AbstractSeqentiaList的
那么我们不妨看一个小例题
A. java.io
B. java.util
C. java.awt
D. javafx.application
A: B
因为在util中,我们有:Serializable, Cloneable, Iterable
T or F?
A: F
LinkedList 和 ArrayList是两个完全不一样的东西
虽然其中所包含的东西都是数据排序相关,但是数组只是用来储存数列的一个东西,链表是数列中的元素首尾相连,看似是数列但实际的又不全是数列
T or F?
A: T
Iterator 迭代器和我们值钱提到的抽象类类似,我们不需要知道它的工作原理,只需要创建和使用就可以了
关于Iterator 相关的操作,最常用的是
next()获得序列中的下一个元素
hasNext()检查序列中是否还有元素
remove()将迭代器新返回的元素删除
所以,我们大可使用一个 for-each循环来执行一些操作
Iterator<String> iterator = lst.iterator();
//iterator.hasNext()如果存在元素的话返回true
while(iterator.hasNext()) {
//iterator.next()返回迭代的下一个元素
System.out.println(iterator.next());
}
引用来源:https://www.cnblogs.com/xiaozhaoboke/p/11038893.html
A. int[] number
B. double[] array
C. ArrayList
D. Float[] f
A: c
嗯这个就是ArrayList的优点之所在了
其他类型的数组我们在创建之初就确定了它们的大小,一般来说是没办法改变的
但是ArrayList可以很方便地在数组末尾添加新的元素
A. The LinkedList provides a singly linked list implementation of the List.
B. The advantage of using the LinkedList is that insertion of new items and removal of existing items is cheap, when the position is provided.
C. The LinkedList is not easily indexable.
D. Class LinkedList is in package java.util.
A: BCD
正确的三项都没啥好说的,错误的A项中,LinkList是双向链表结构 Doubly Linked List
那么,假如有这么一个例题
如果要实现下面这种数组的排序效果,应该用什么样的思路捏
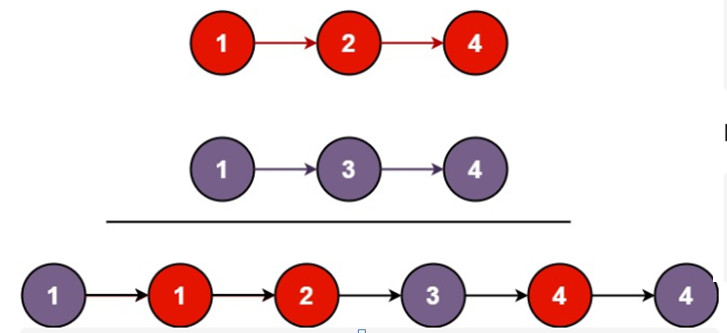

嗯是不是你也没想到
是的没错我也想太多了
这里的就是一个简单的思路
并没啥幺蛾子
那我们不妨在看一个例题
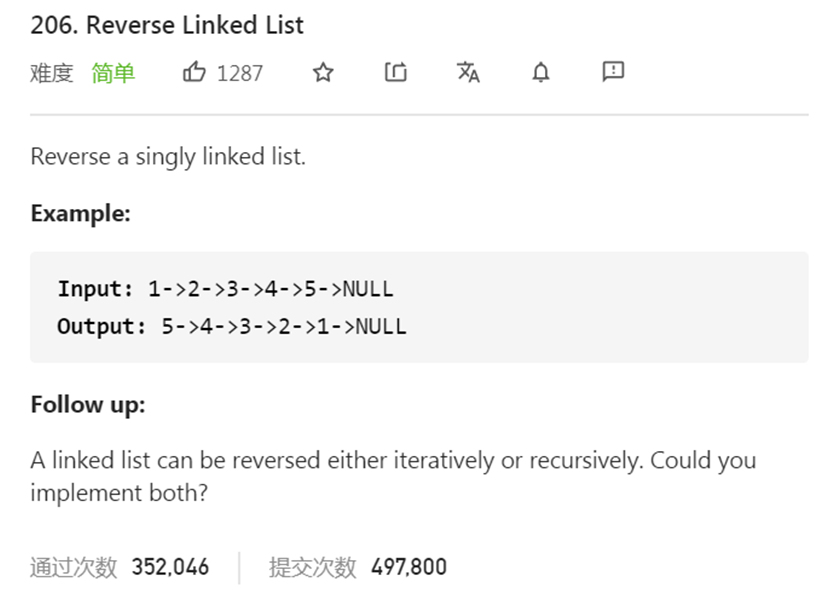
在上面这个例题中,我们需要做的就是翻转数组
这个的难点在于Null的位置,你看假如我们翻转整个数组,Null从数列的尾部到了数列的头部
要翻转数组的同时还不能改变null的位置,我感觉这个是一个比较有挑战性的题目
再看一个例题,如果说我们需要删除特定的一位数字,比如需要达到一个这样的效果
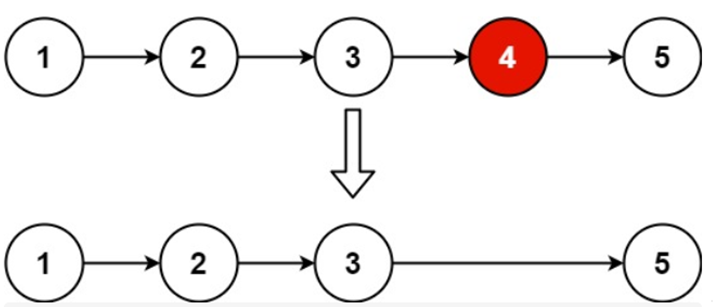
不妨去思考一下代码
好的女士们先生们,接下来让我们来看看栈的抽象类型 Srack ADT
栈是一个列表,我们限定只能在其顶部 TOP 增加或者删除元素
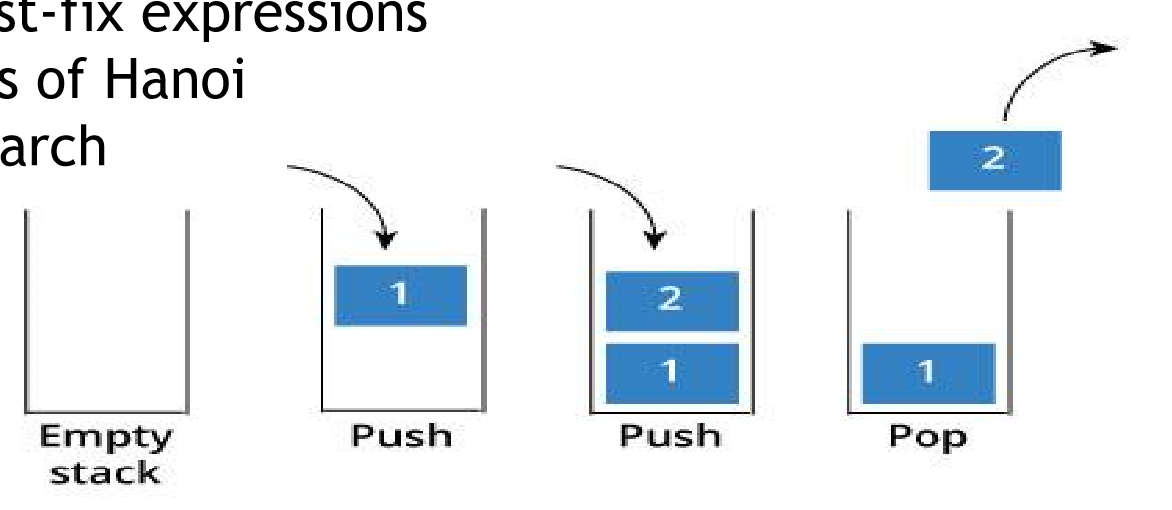
我们以前学过,栈遵循着LIFO (last in, first out) 的原则,在这里加两个基本操作,push 和 pop
Push 推 就是插入一个元素
pop 删除 就是删除最考上的一个元素
也就是说,如何使用列表的方法来实现栈的效果
一般来说我们可以使用一个 singly linked list 单链表 来实现
之前我们讲到过,链表中,我们有 push 操作和 pop 操作
那我们使用单链表的时候,可以在列表的前面插入一个元素来实现push操作,同样也可以删除前面的一个元素来实现 pop
之前我们也讲过,Strack 就像一个桶一样,只能从上面往里面装东西所以当其中没有东西的时候,应该返回一个null的值
对于栈的性质这里就不多阐述了,对于Array of Stack来说,我们需要注意的是两个元素
theArray 和 topOfStack ,对于空的栈来说他们的值为-1
因为对于栈来说,唯一值得在意的不过是数组本身和最上面能够存取的那一个元素罢了
如果这个栈的值为空的话,topOfStack的值应为 -1
为了将元素 x 推进(push)栈中,我们可以增加topOfStack的值(比如 topOfStack += topOfStack + 1),然后使用 theArray[topOfStack] = x
对于将元素 x 弹出(pop),操作也是类似的。一般来说通常的操作是减少topOfStack的值,也就是最上面的这个元素应为没有与其对应的数组中的index,就会被删除掉了
那么你可能会问,既然java中有LinkedList,那有没有栈相关的class呢?
嘿,你别说,还真有
Stack在java中是Vector的子类,一般来说我们可以导入包然后使用该方法
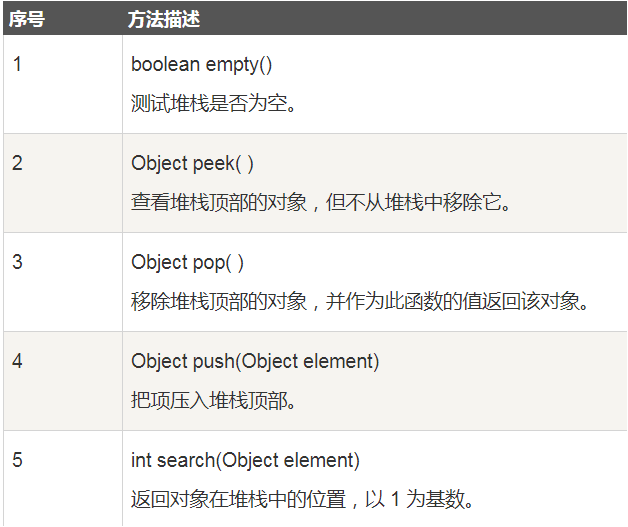
你知道套娃嘛
那么我们如何处理一串类似于“[(({}))]”这样子的字符串,判断其匹配是否合法呢?
'('与 ')'、'['与 ']'、'{'与 '}'。如果符号没有按照对应方式嵌套匹配,则认为匹配非法。
简单的来说,就是如果我们需要往栈里面推进去一组括号的话,那这组括号必须是相互对应的
你不能说只有一半的括号,这样子的括号是假的
这里引用:https://www.icode9.com/content-4-611366.html的一个示例用小程序
int Judge(char s[]) {
int len = strlen(s);
STACK stack = CreatStack(len);
for(int i = 0; i < len; i++) {
if(s[i] == '(' || s[i] == '[' || s[i] == '{' || IsEmpty(stack))
push(s[i], stack); //为左元素或栈空,入栈
else if(IsMatch(top(stack), s[i]))
pop(stack); //与栈顶匹配则栈顶元素出栈
else
push(s[i], stack); //与栈顶不匹配则入栈
}
if(IsEmpty(stack))
return 1; //栈为空,说明完全匹配
return 0; //栈不空则说明有无法匹配之处
}
也就是说,每一个入栈的符号,凡是左元素(左括号之类的)的就允许入栈,右元素想要入栈的话就必须检查前面有没有与之对应的右元素
如果没有的话,是不允许入栈的
当我们在方法中声明一个变量的时候,这个变量就会在系统中分配得到一些内存,这些本地变量都是由系统保存的,但是当我们调用新方法的时候,之前方法中的本地变量就被其他的东西给替代掉了,也就是说消失不见了
但是我们可以使用一个栈来储存一些变量,因为栈是一个栈内存,是一个动态储存的区域,由系统自动分配的,一般来说速度都很快。
并且,我们可以将一些数据容易溢出的数据放在栈里面,这样对于程序来说也是一个很不错的主意
比如,我们可以来看一个小栗子

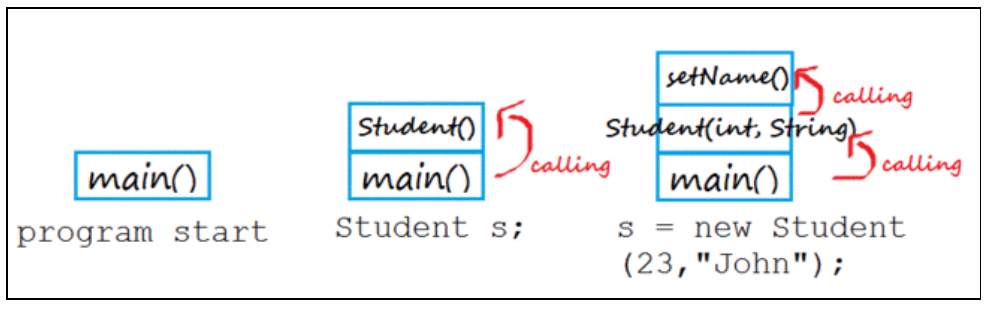
机智问答:为啥这一块是红色框起来的
那当然是因为——————
这地方必考啊
别问我怎么知道的
这里的定理就不多阐述了,用一张图来表示的话就是:

一般来说,这个东西说白了就是倒过来倒过去,在这里需要了解3个名次
Infix Notation (人能看得懂的)
Prefix Notation / Polish Notation 波兰表达式 (不是给人看的)
Postfix Notation / Reverse-Polish Notation 逆波兰表达式 (不是人看的)

注意,Prefix Notation和Postfix Notation的区别就在于运算符号的位置
嗯,接下来的环节我估计你也猜到了
是的没错就是相互转换哈哈哈哈哈
反正当年算循环代码都挺要命的了,这个。。。。。。好像没之前那个要命
嘿嘿
这样吧,用事实说话(焦点访*)
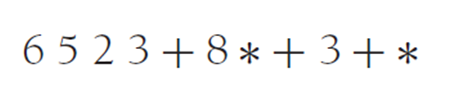
首先,我们先 创建一个栈Create a stack
想要解答这个问题一定要灵活运用栈及其概念才行
因为错一个符号整道题都会错
然后这个基本都喜欢出在解答题......10分的那种
咳咳,言归正传
然后我们需要对算式中的每一个元素进行归类,如果是数字的话就将其推入栈中,如果是运算符号的话就从栈中弹出元素,将其组合成式子
简单的来说,就是
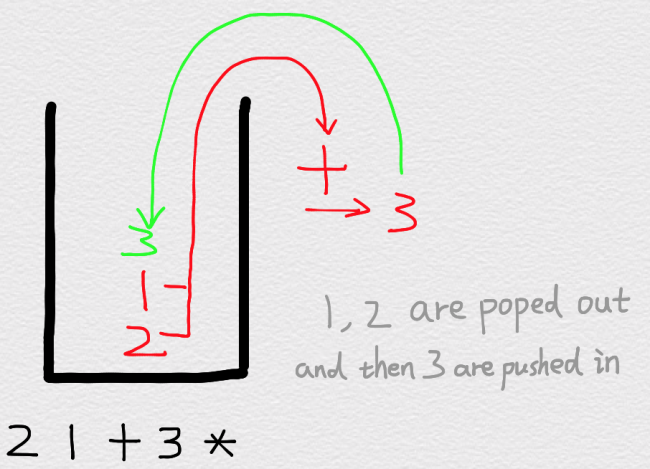
图片来源: https://blog.csdn.net/u012998254/article/details/47020169
最后,待元素全部转化完成之后,得到的就是人能看得懂的式子了
我们再来举一个例子,
5 1 2 + 4 * + 3 −
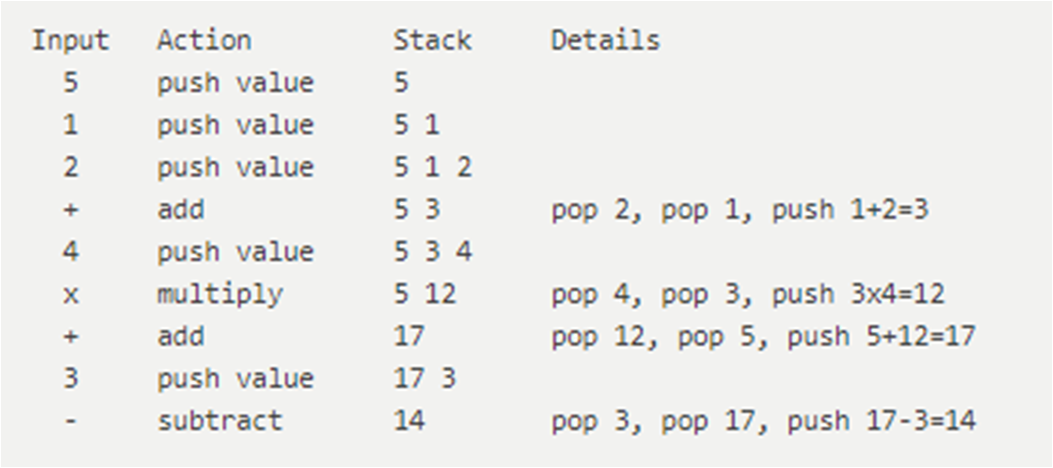
嗯,正向的有了,反向的必须也有
点击下方按钮展开来查看哦
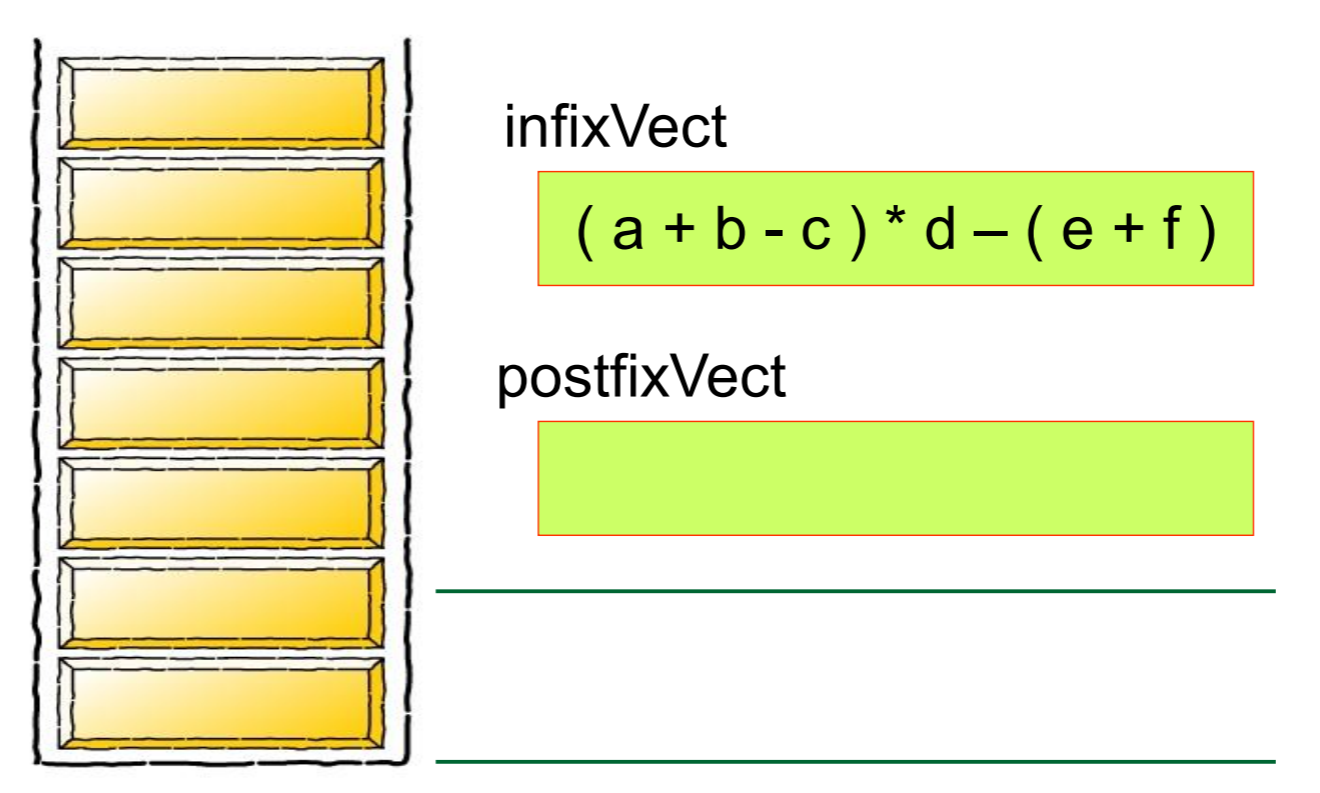
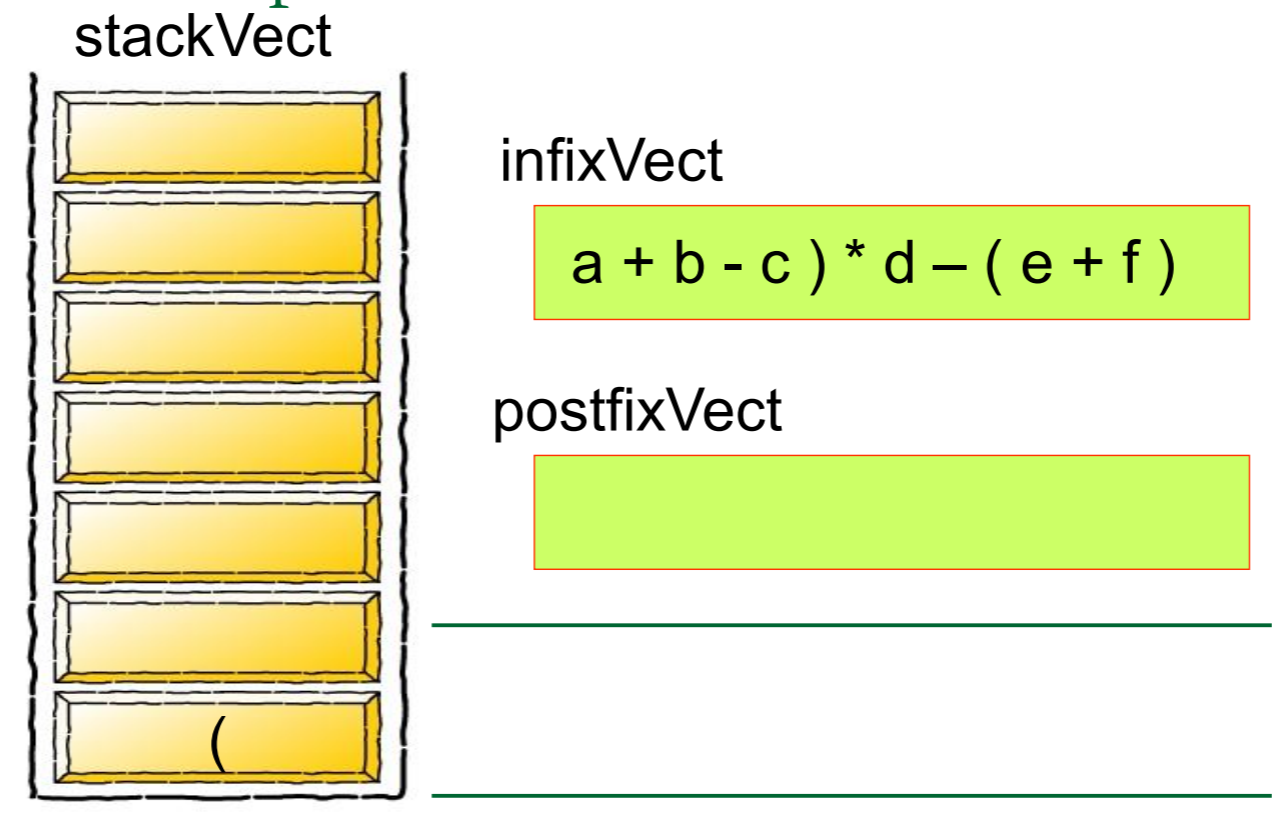
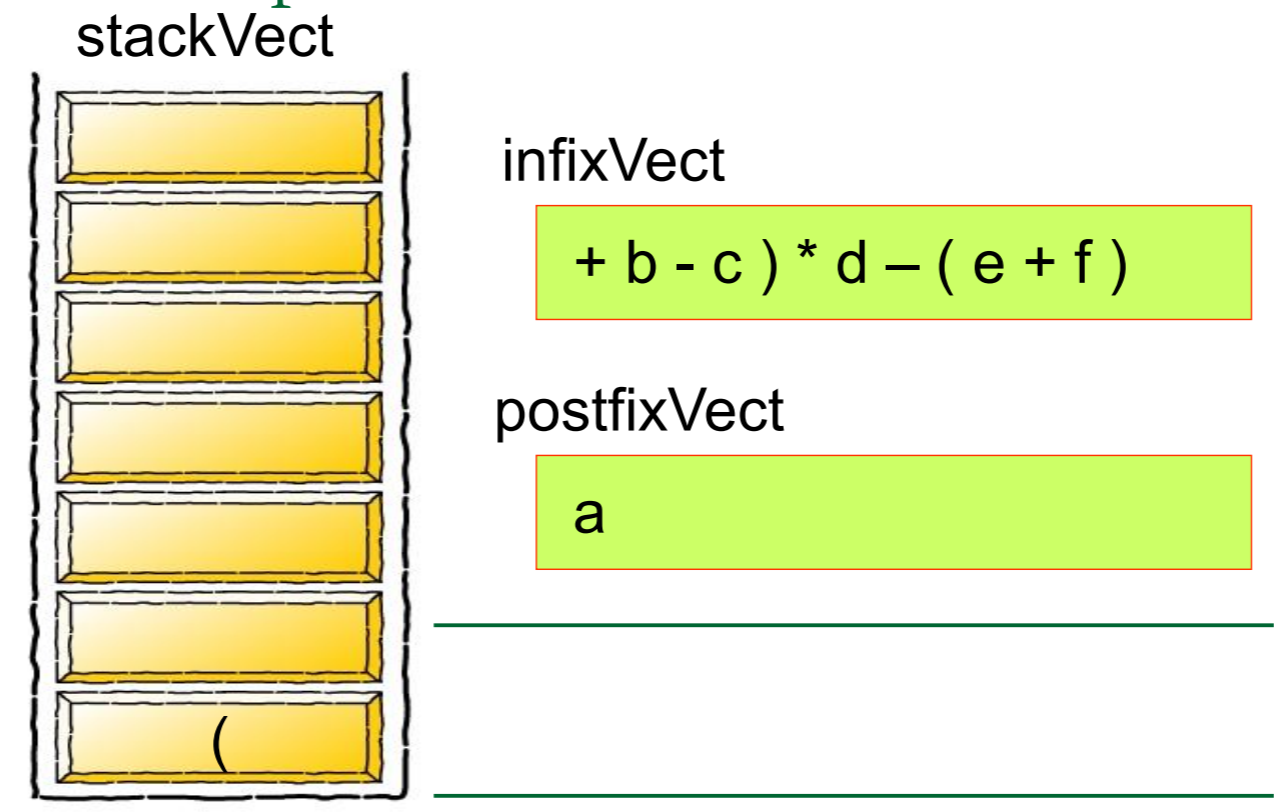
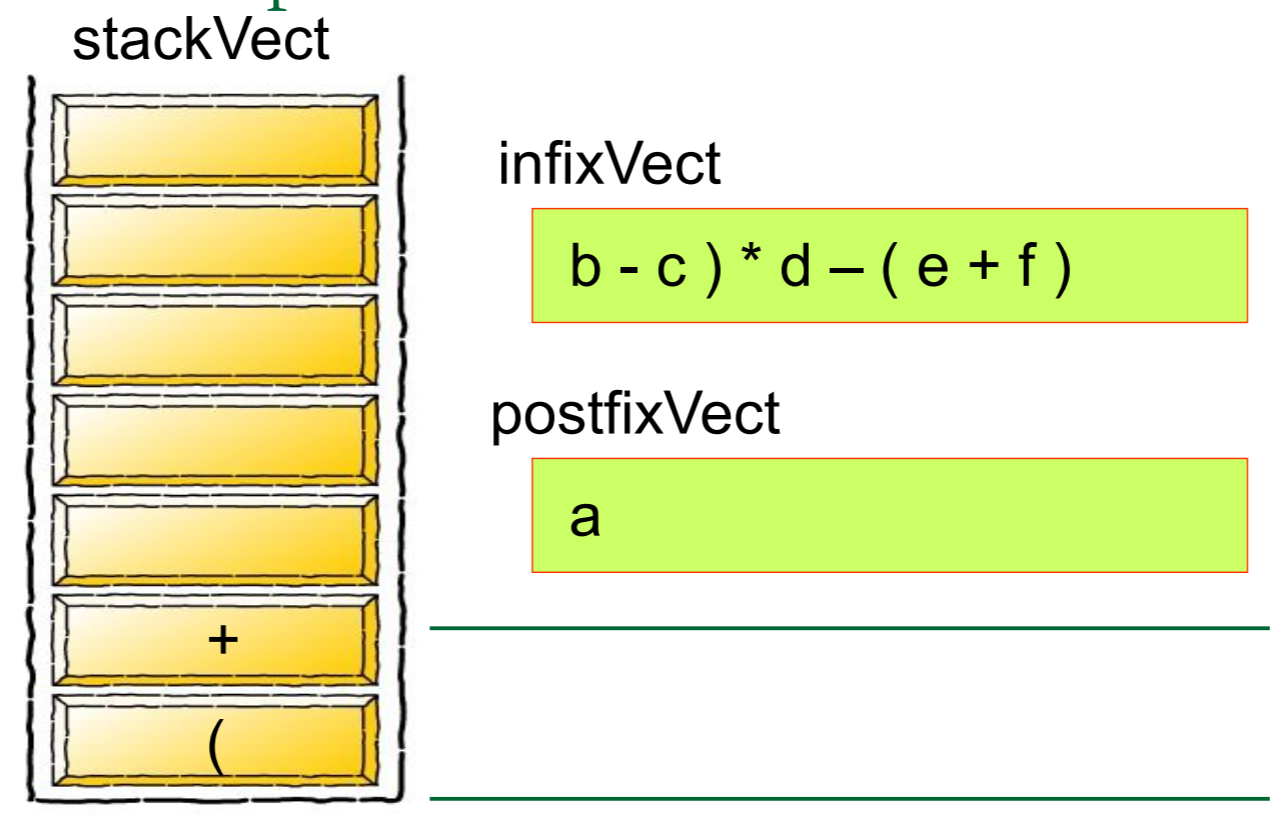
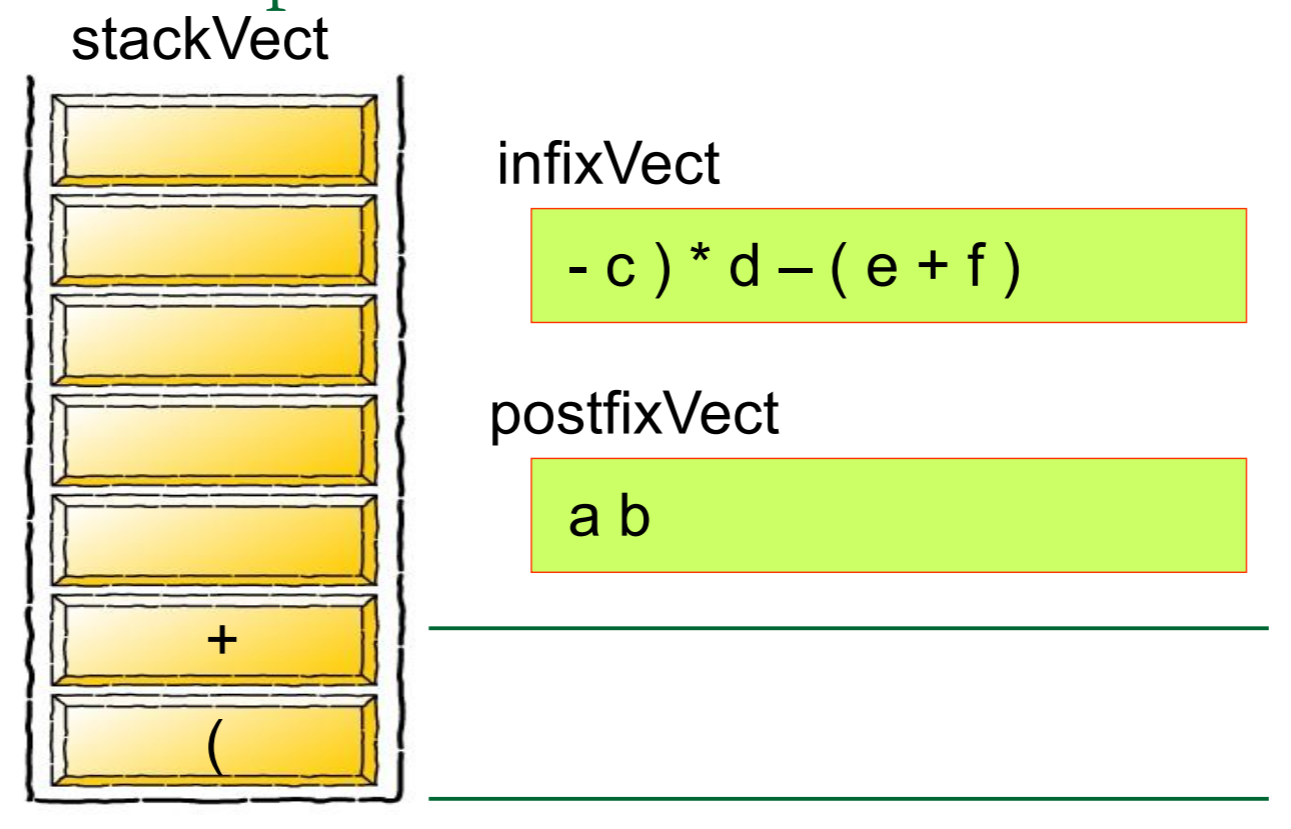
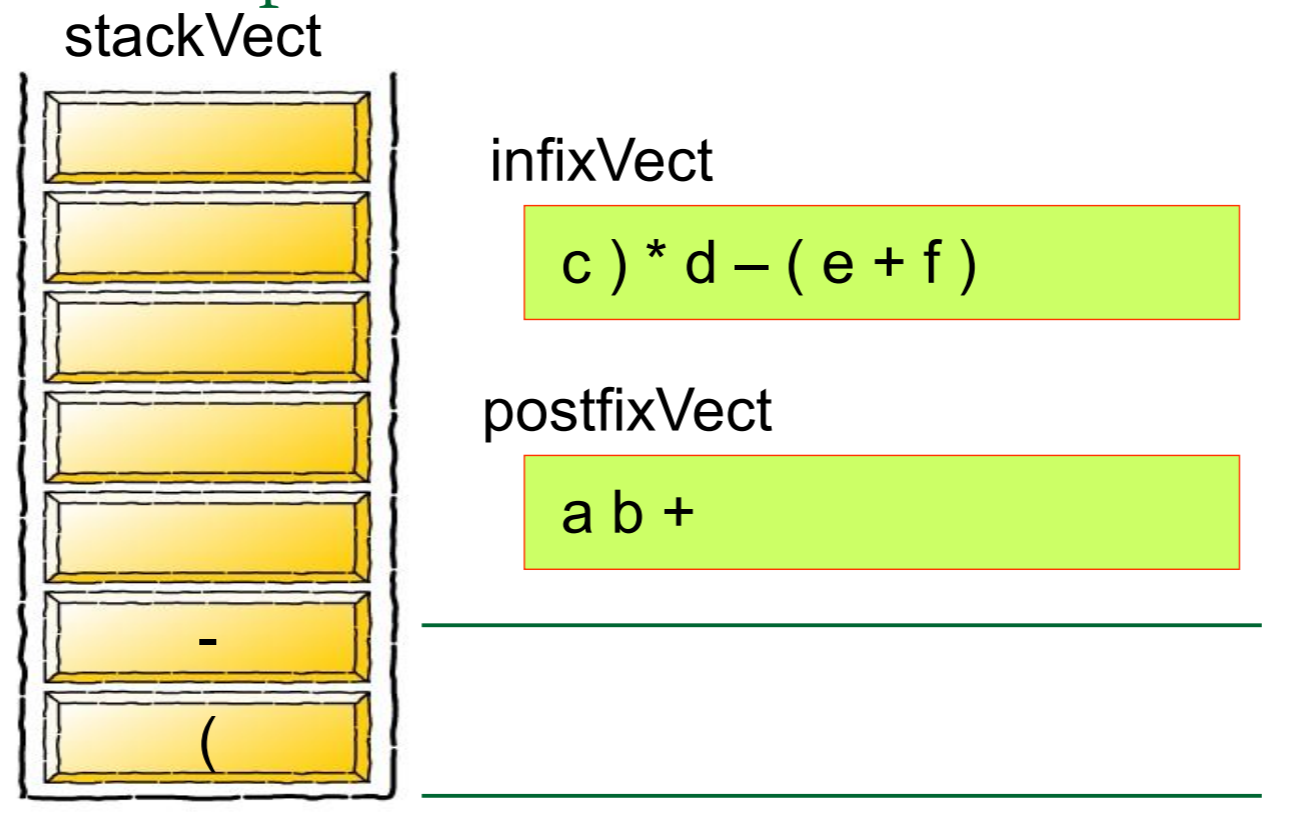
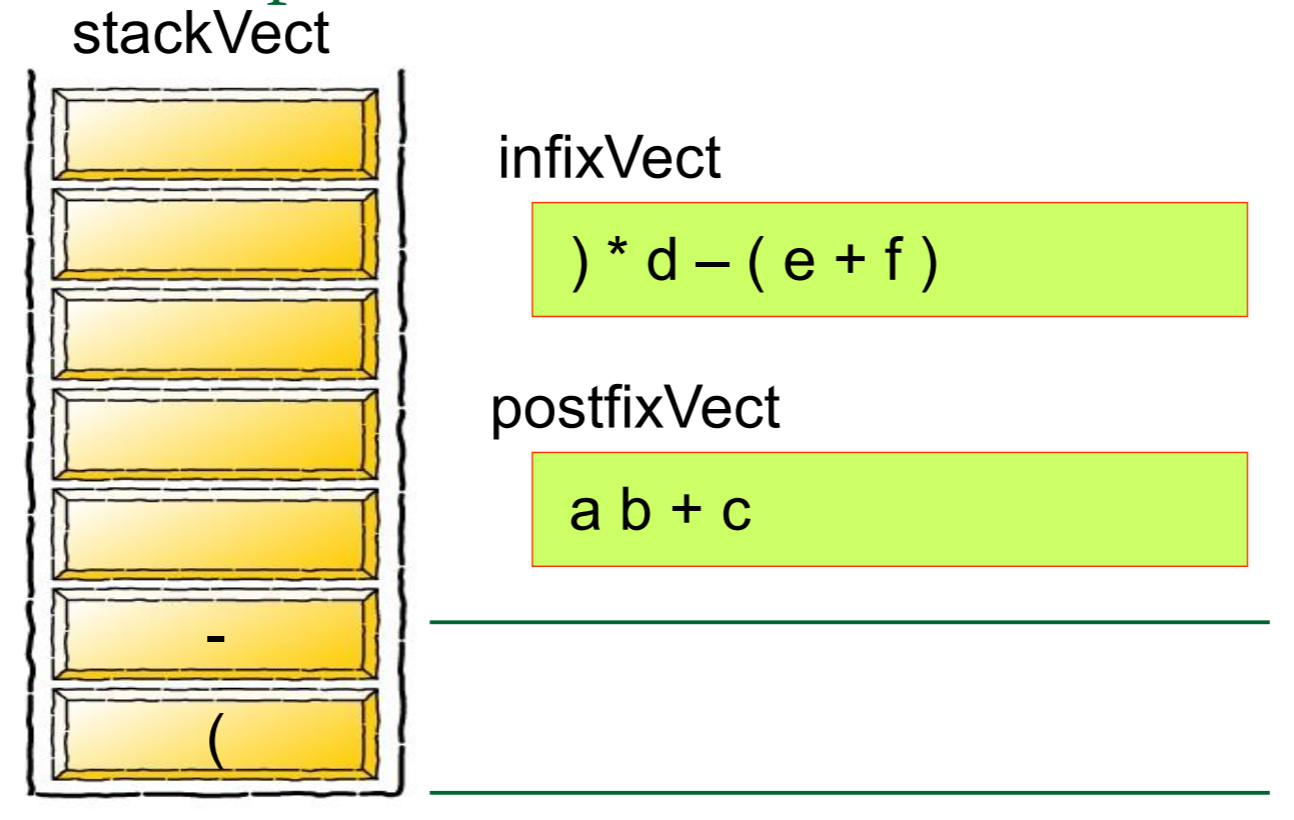
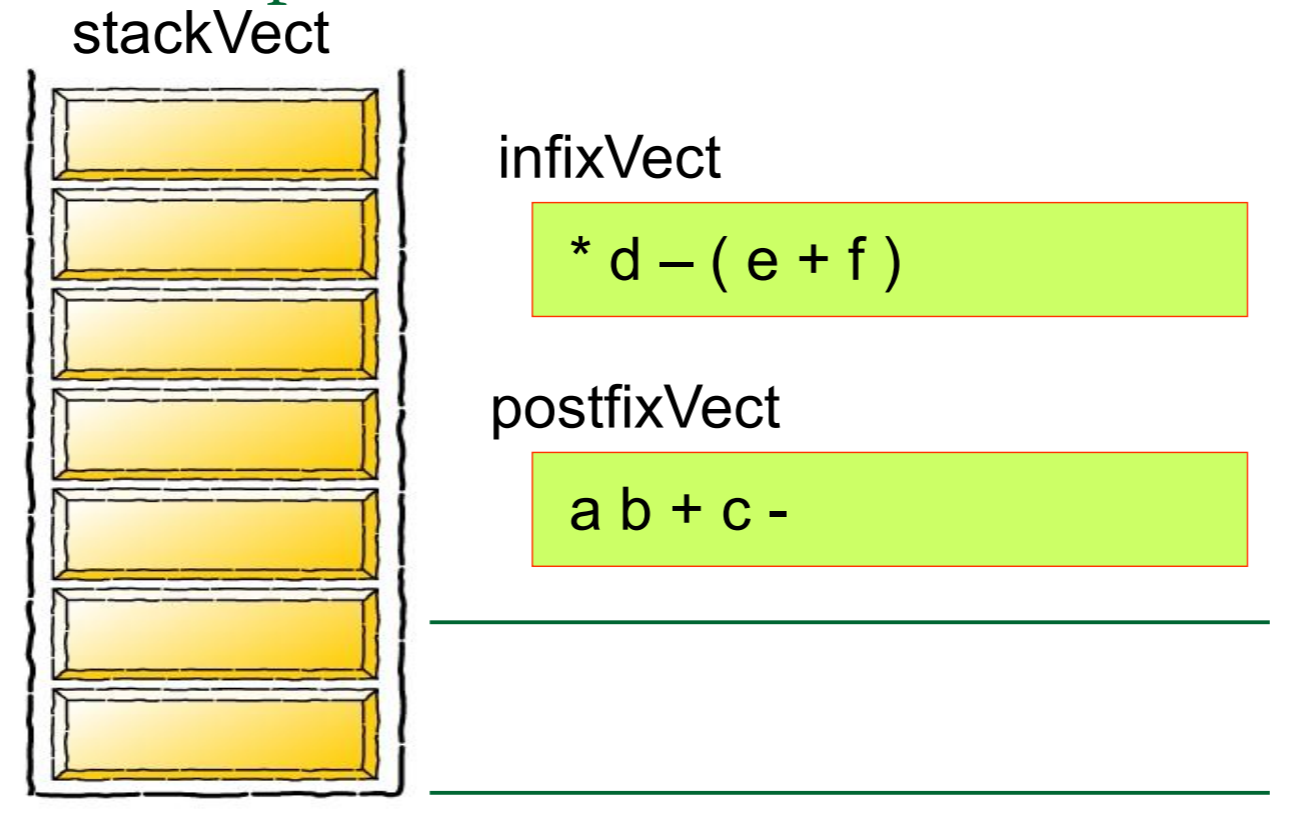
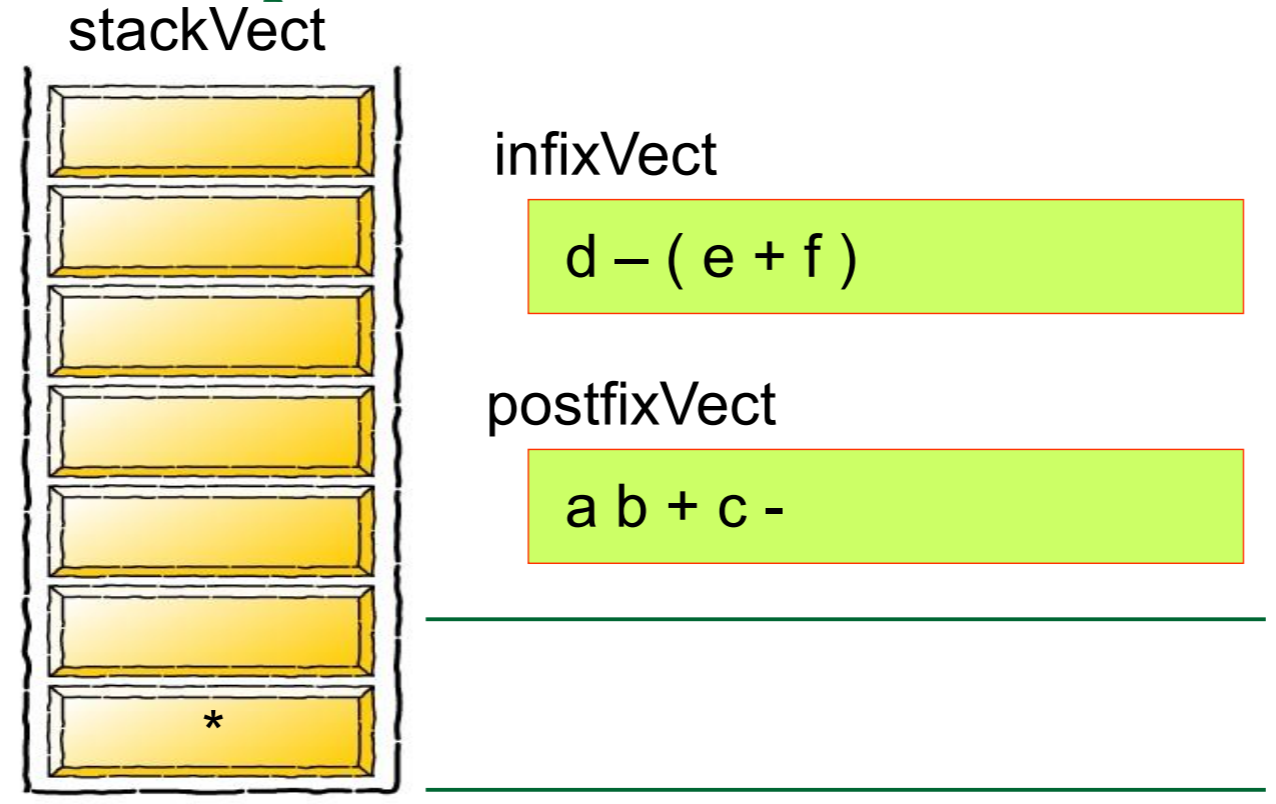
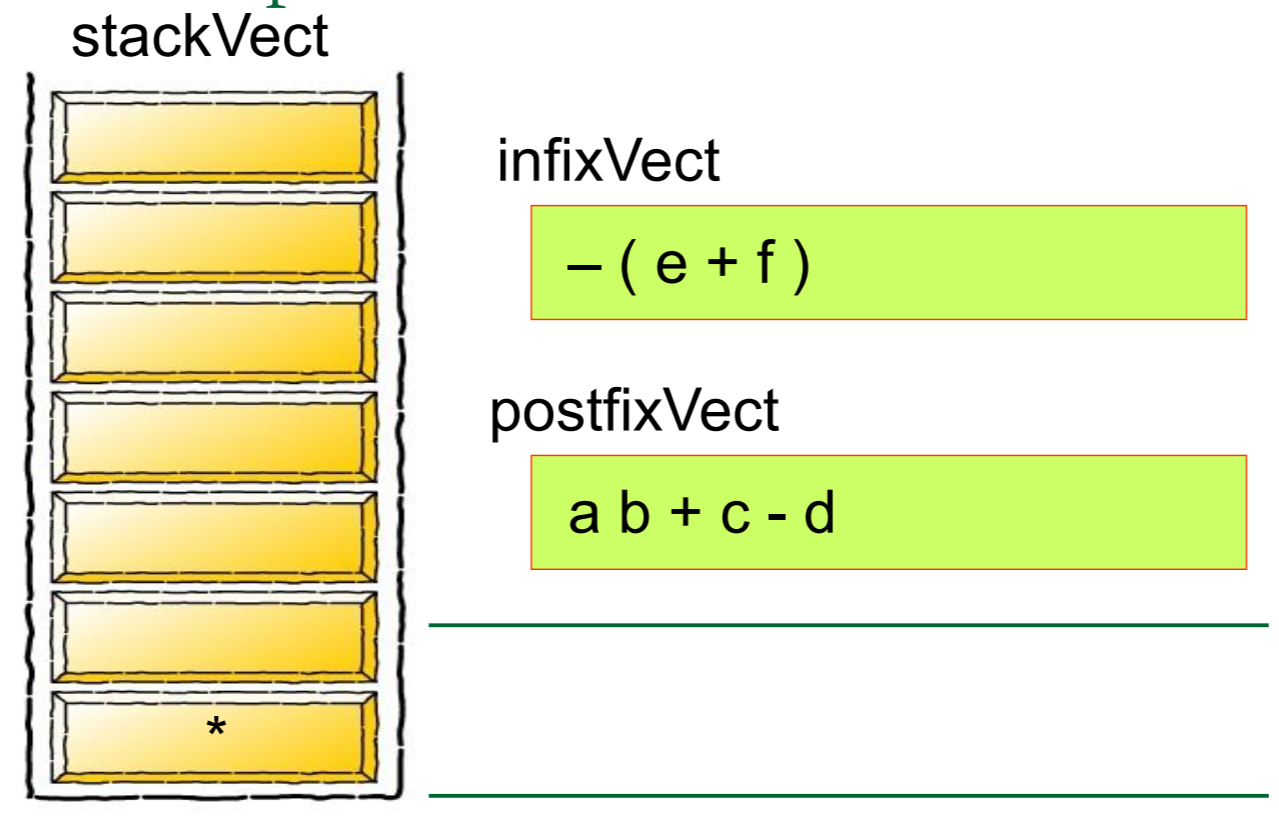
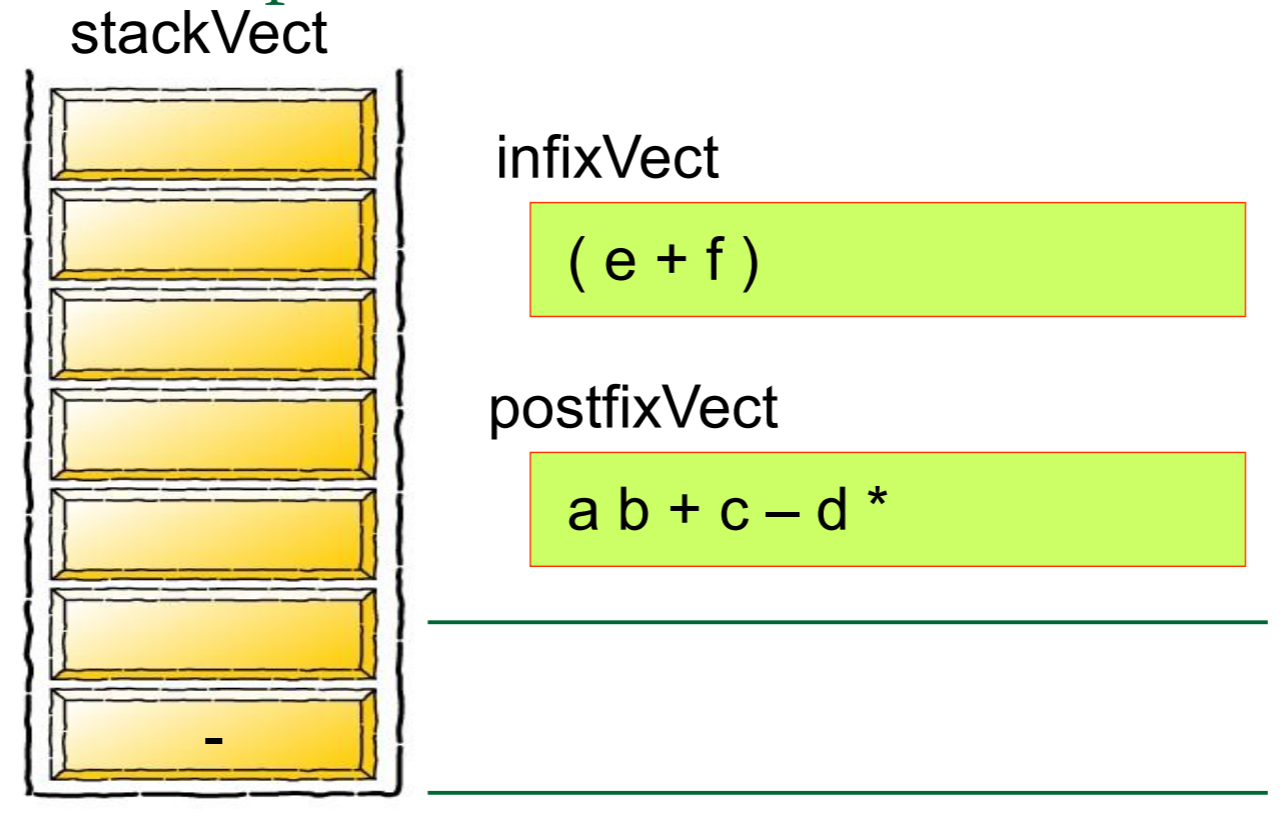
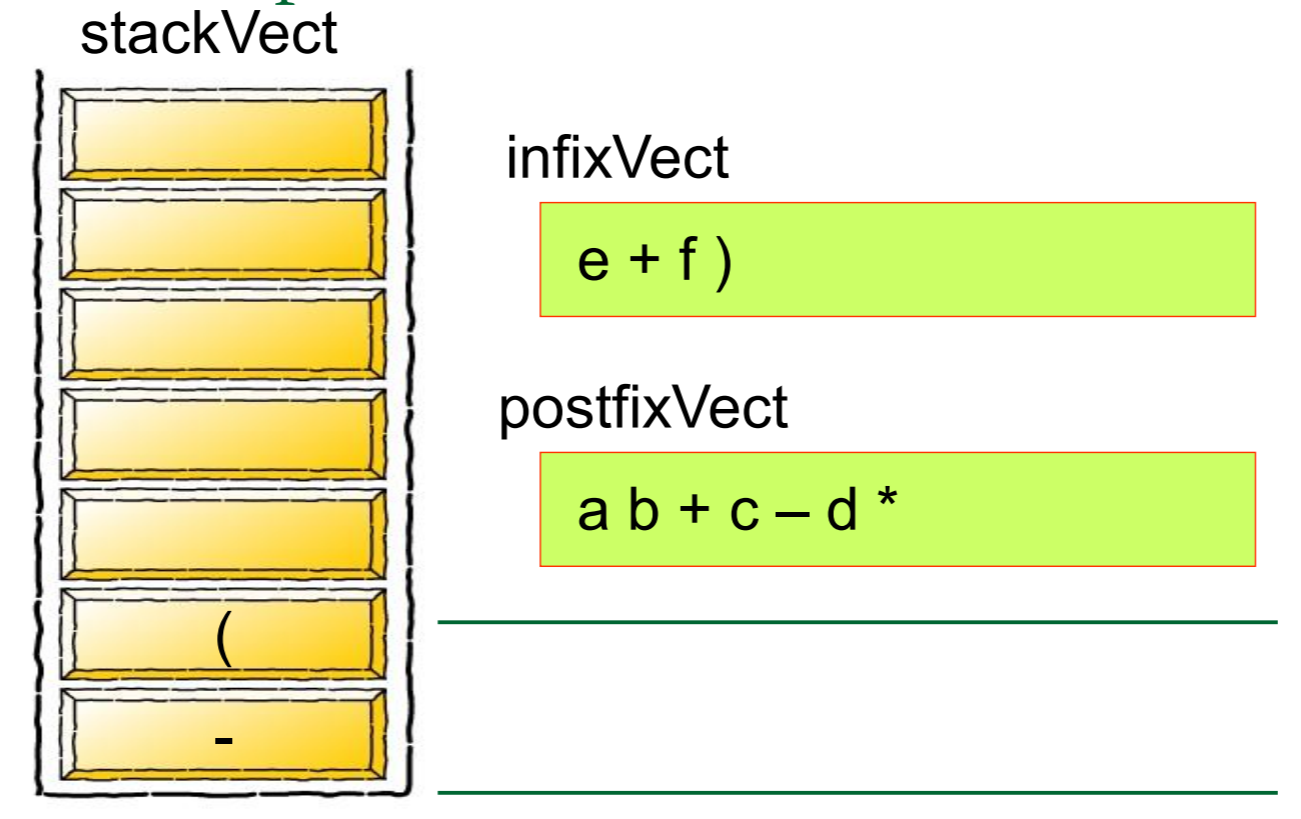
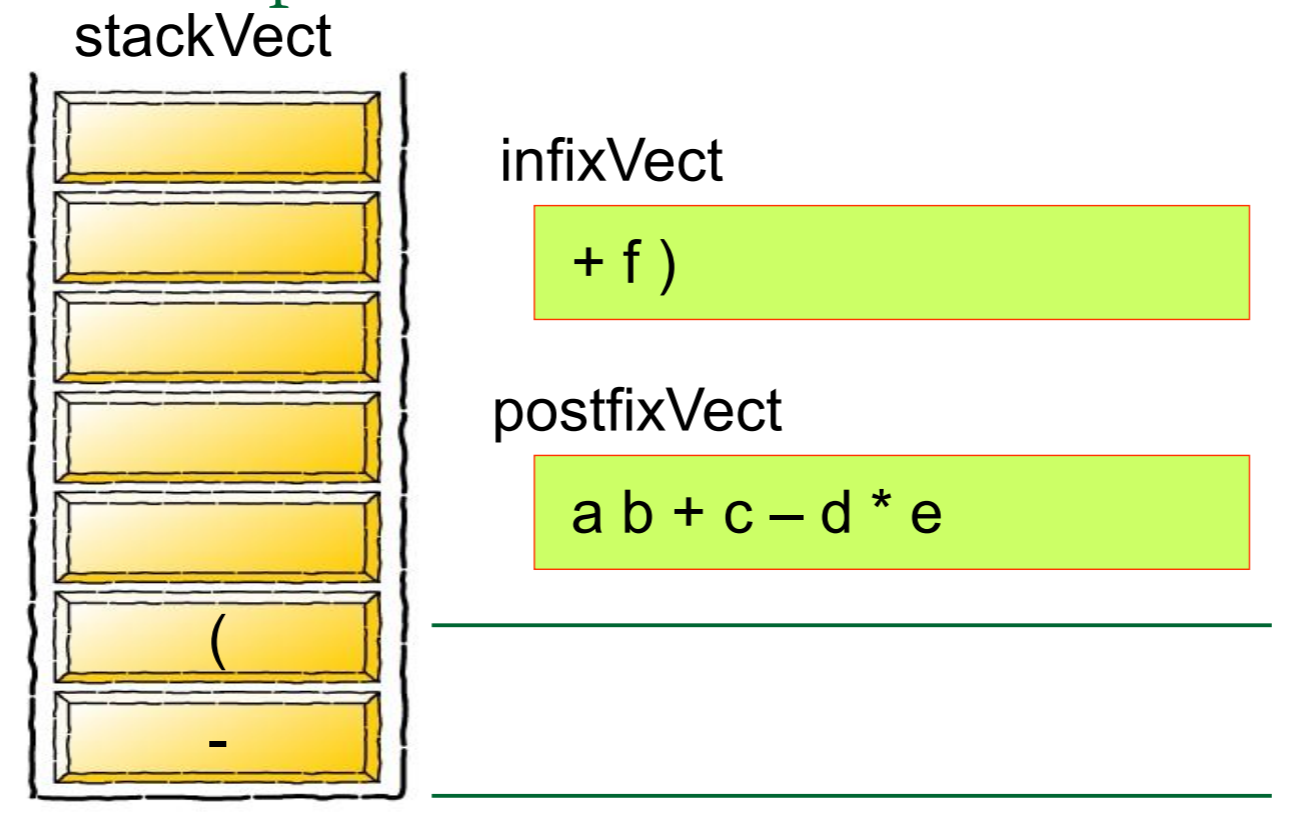
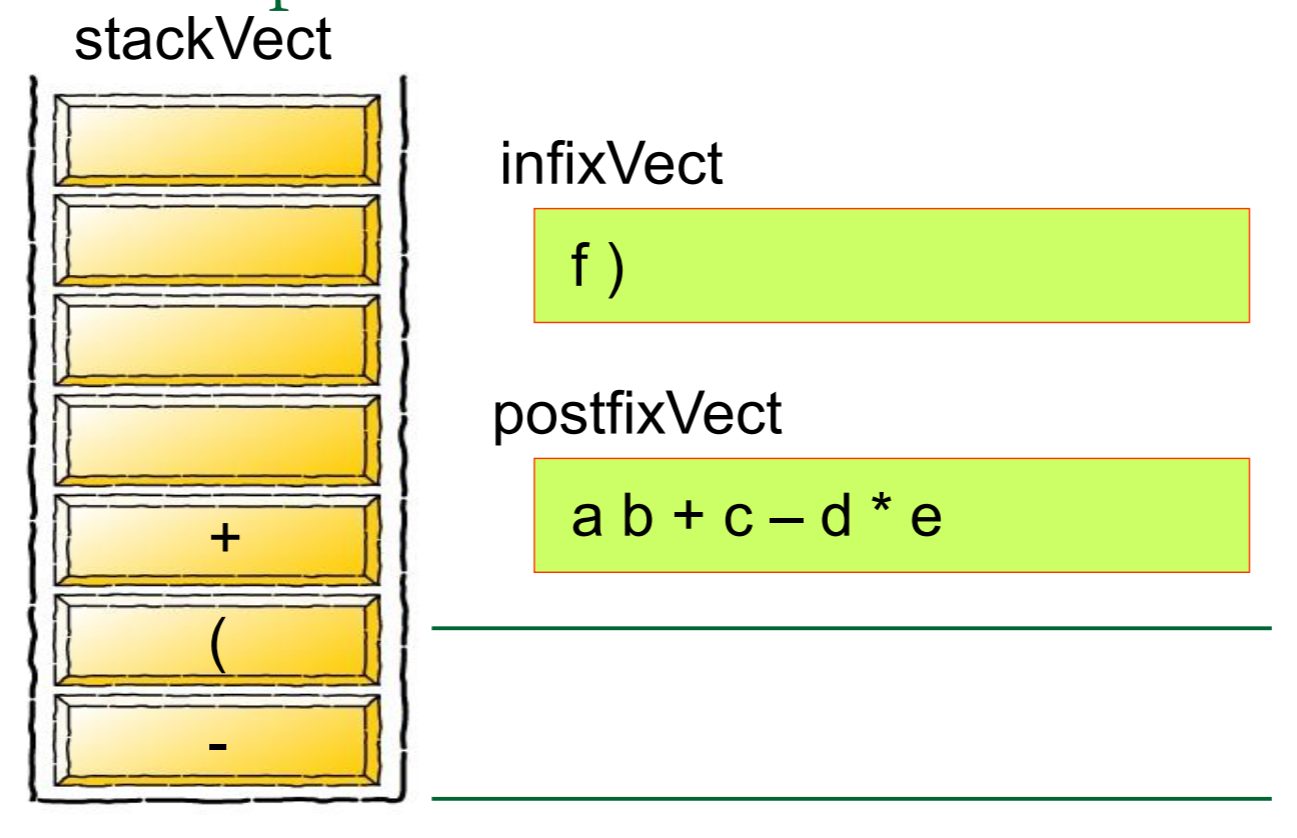
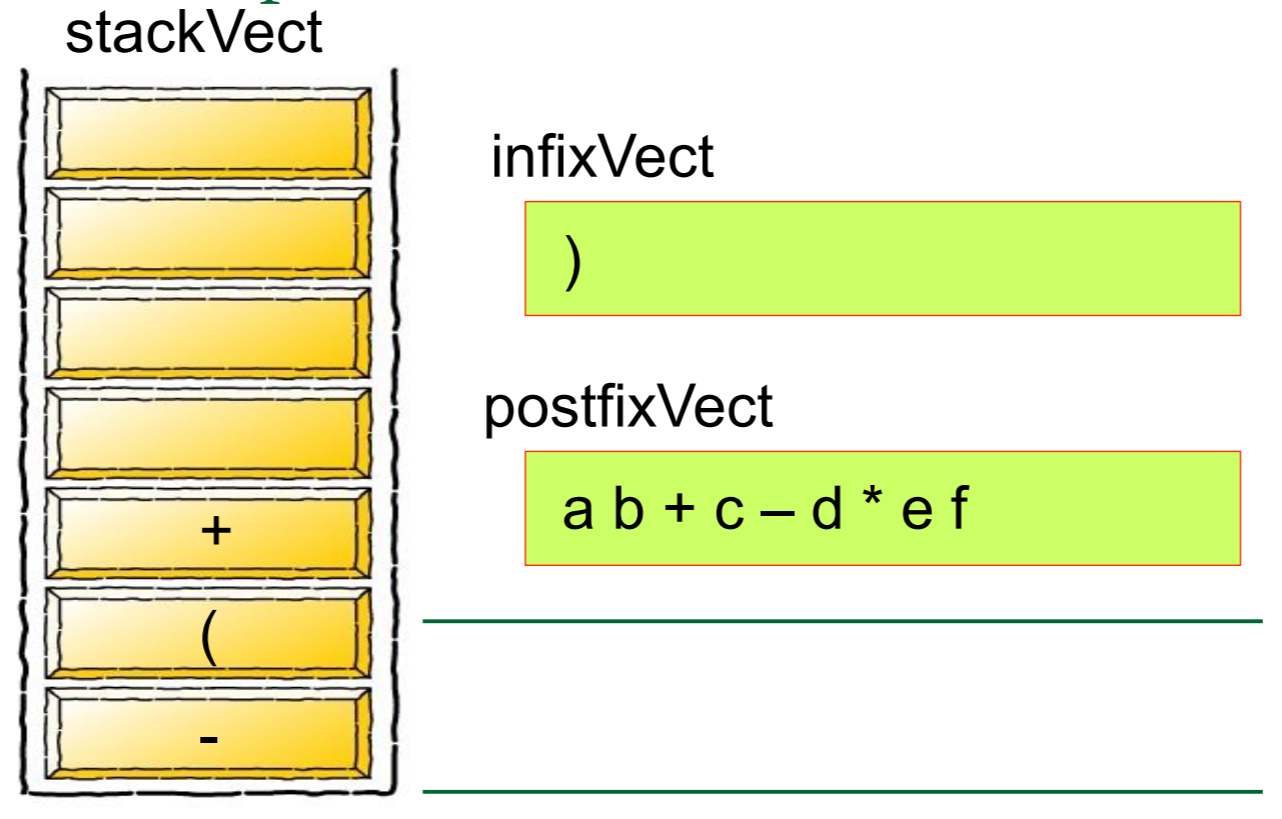
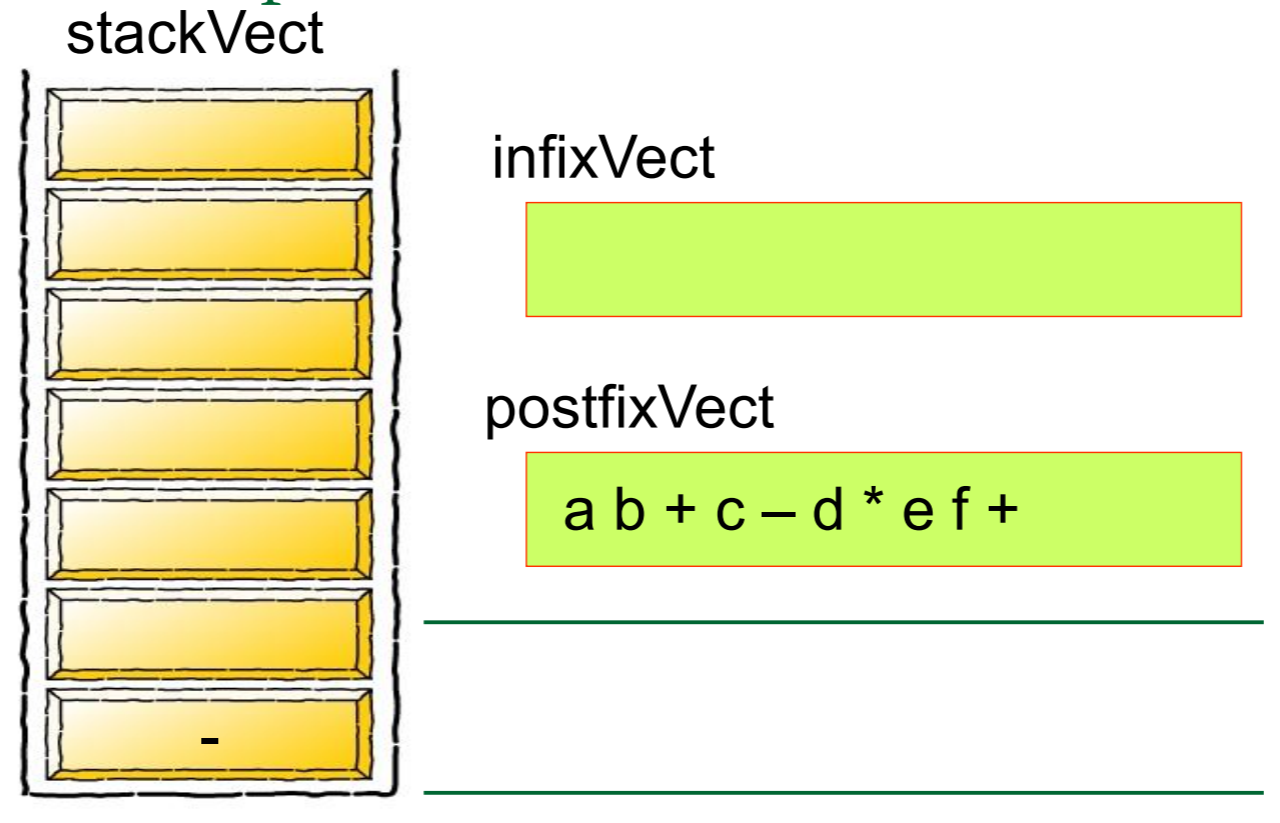
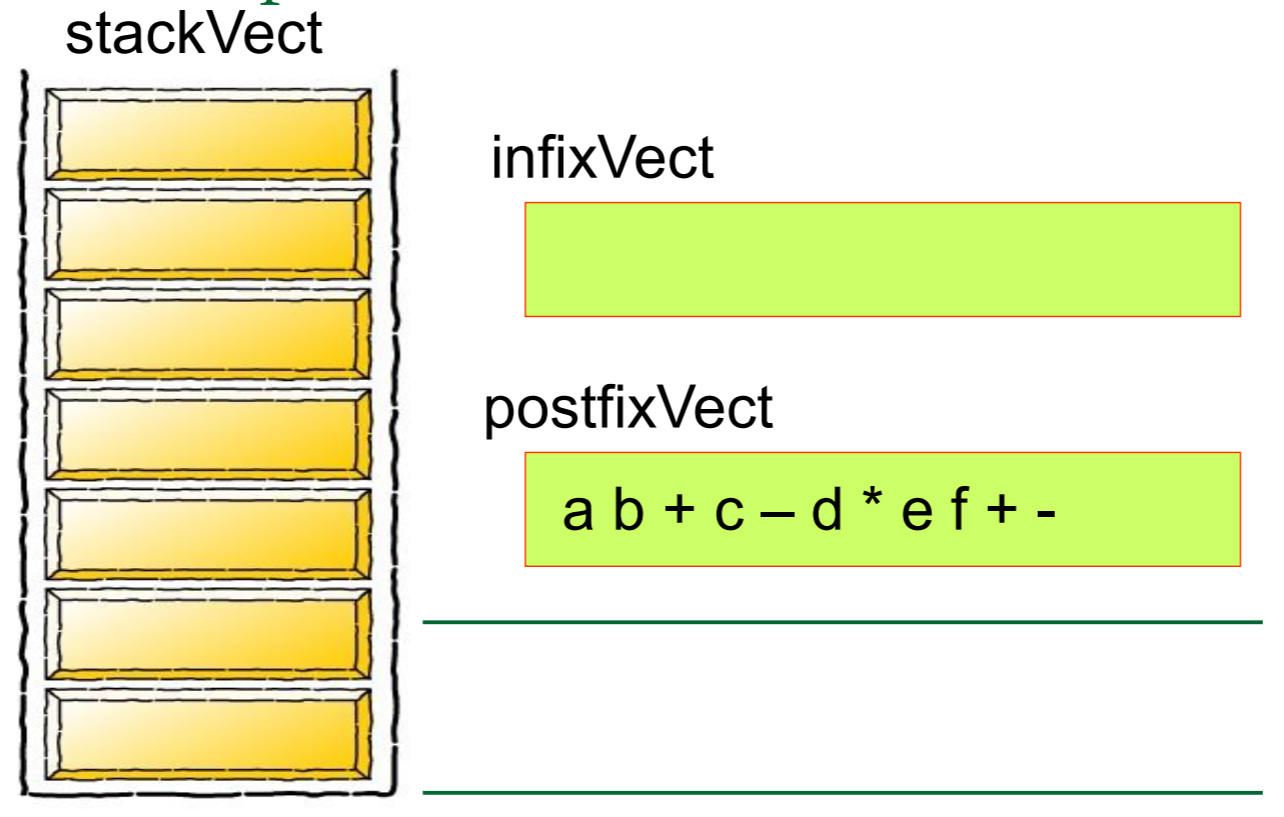
看了眼发现如果倒着看这些图片的话,刚好就是倒过来推的方法
abc+def+*
where a=1, b=2, c=3, d=4, e=5, f=6
A: -19
我猜这里应该有一个方法总结,就是用于概括应该如何推出和反推出来这个东西。
但是我感觉这玩意用文字来表达出来真的挺反人类的
倒不如看图理解的快
所以说啊!仔细看看上面的图吧
记得要结合栈的概念来理解
下面咱们来看一下 Queue 队列
我们之前讲过,在常见的线性结构中,除了栈之外,还有一个就是队列了
看到这个,不难想到排队
其实这玩意和排队还挺像的
这个在咱们的现实生活中,比如打印机的打印队列就和这个很相似
队列和栈一样,都是一维数组
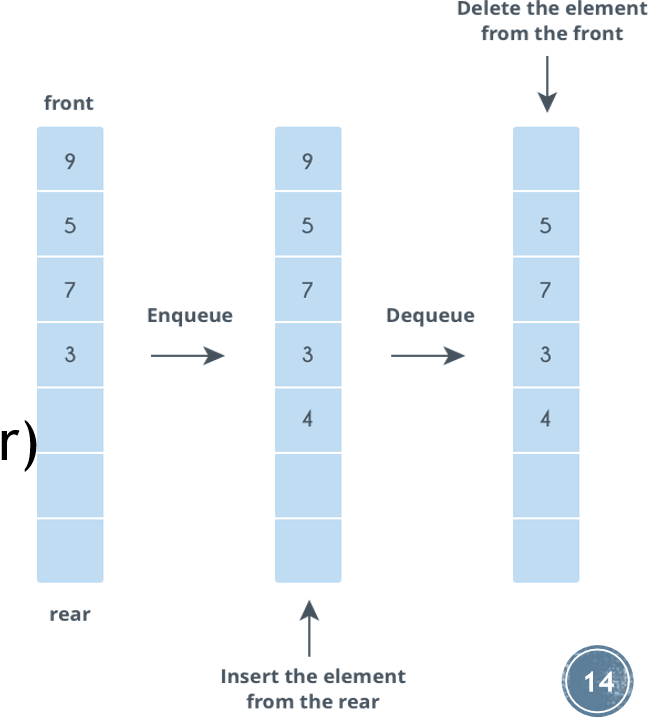
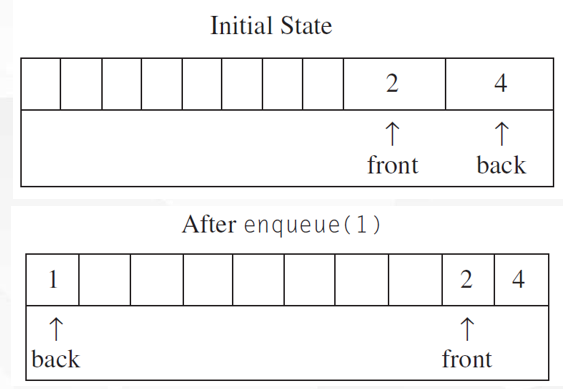
队列的基本操作包括: enquene 入队、dequene 出队
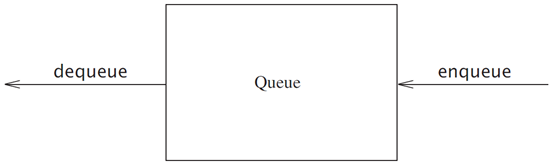
所谓入队就是在列表的末尾 rear 加入一个元素,而出队就是弹出列表最前端 front的元素
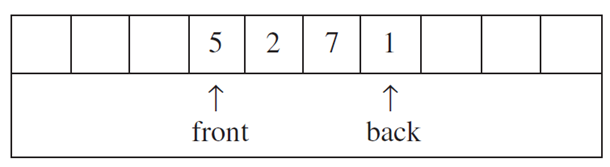
对于队列来说,加入是在一端完成,而删除是在另一端完成的
我们将元素从队伍的末尾加入,称之为入队。用伪代码来说的话思路大概是这样
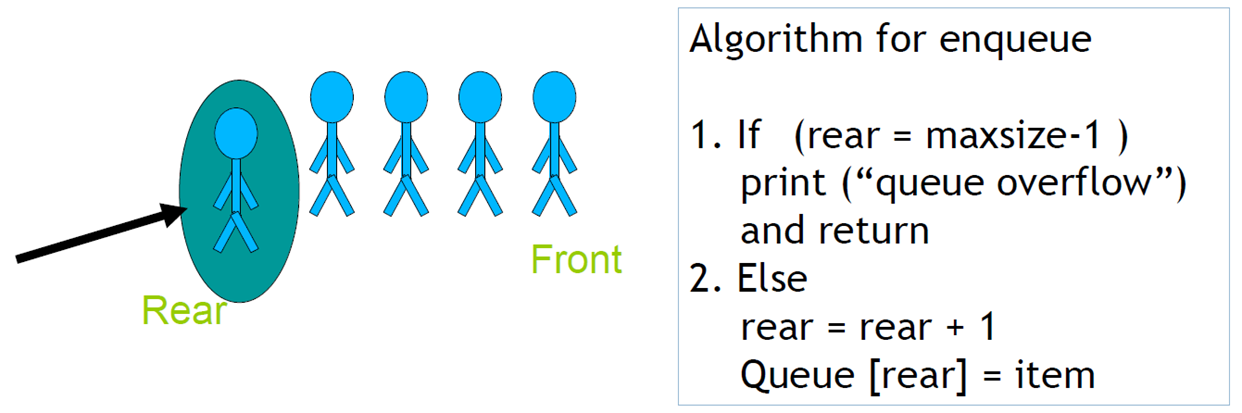
同样的,当队伍弹出一个元素时,我们称之为出队dequene,出队是在队列的前面操作的
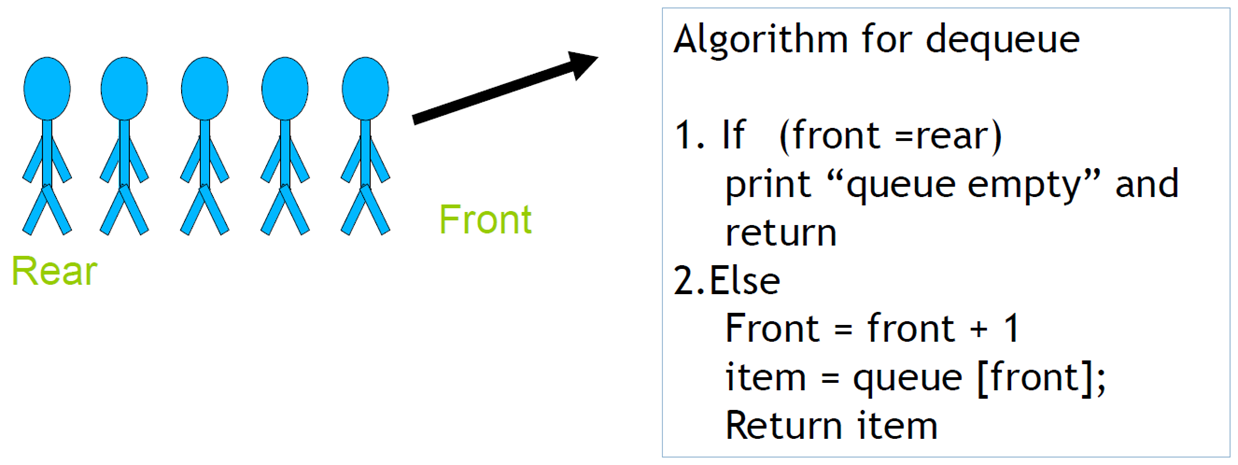
哦对了,你有没有想过一个问题
假如我们一开始规定了一个数组,这个数组的大小已经被声明了
那我们不停的改变其中的元素,front和back就会不停地移动
那么当他两碰到一起的时候呢?
有个叫做 循环数组 circular array 的玩意可以很好的解决这个问题
只要前端或者后端达到数组的末尾,它就会自动回到数组的开头
Chapter4: Trees
emmmm
其实嘛
你要说树就是咱们平时生活中的大树
好像。。。。也没错!
因为树这种东西有许多的分支
也正是因为它有着许多的分支,它就不是线性结构啦
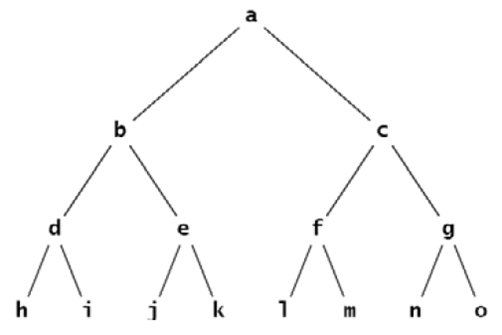
一般的,我们可以称树是 节点 Node 的集合,集合是空的也是OK的
树一般由一个管理员帐号 root 根 和 许多的 T1、T2、T3....分支
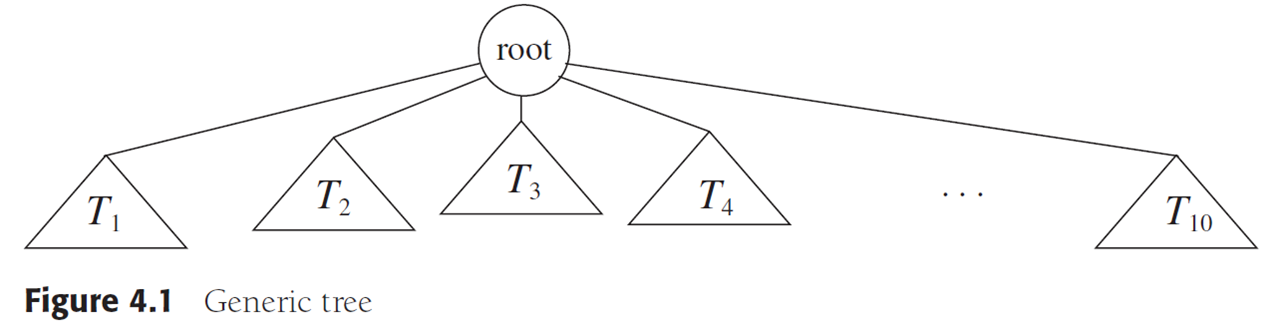
根和这些分支之间都有相互的连接
每一个 子树 subtree 的根被称为 r的 子代 child
相对于的,r就是这些树根的 父类 parent
- 每一个节点都可以有任意数量的子代,也可以为零
- 没有子节点的节点(就是往下再延伸的节点)称之为 叶子 leaves
- 具有相同父节点的是同级节点
PS: GroundParent节点也可以用类似的方法去定义
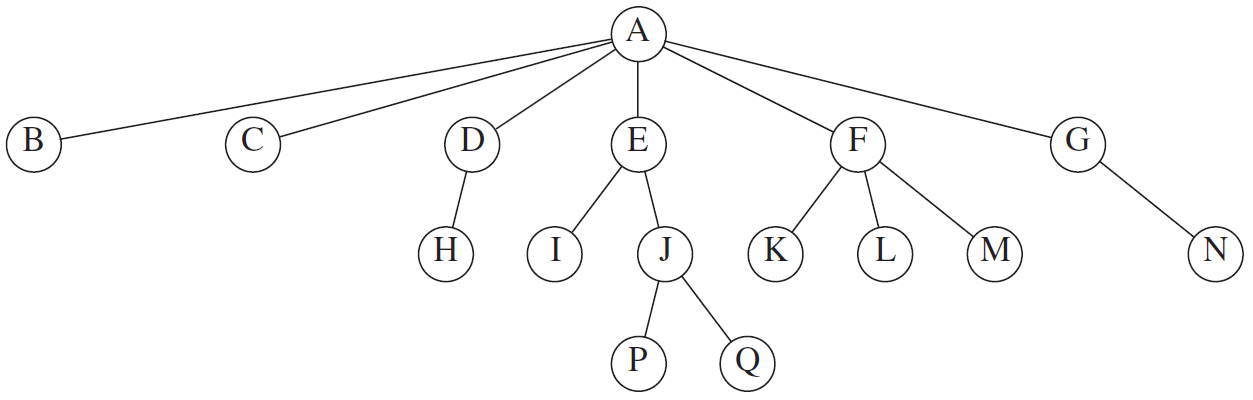
嗯我想你也差不多猜到了
这玩意怎么可能少得了计算题?!?!?
那必然不可能
所以,让我们来看看树的计算:
emmmm
这样吧,我不说定义了
咱们直接上实例
首先你先看之前讲定义的那张图
这里的E处于高度 height 1, 深度 depth 1
F处于高度 1,深度 1
树的高度是 3
嗯能理解了嘛
我们不难总结出,对于任何的节点,我们可以设为Ni
Ni的深度是从根到Ni的唯一路径的长度
顺带一提,A所处的高度为0
也就是root的高度为0
然后Q所处的高度也就是树的高度,也就是3
假如存在N1 到 N2 的路径,那我们称 N1 是 N2 的祖先 ancestor , N2 是 N1 的 后继 descendant
你还别说,这玩意我们可以玩出话来
比如这样
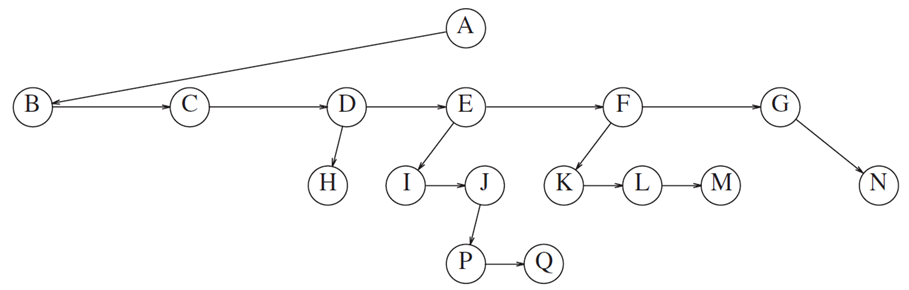
你看上面这个就是尤其的皮
不难总结出,我们应该将每一个节点都串联在一起
不应该出现没有连接的节点
那假如这个时候我问你,如何用代码来把上面的这个数实现出来呢?
其实不难发现,他们之间有个层级关系
class TreeNode
{
Object element;
tree firstChild;
TreeNode nextSilbling;
}
一般来说,我们可以使用TreeNode类来定义每一个节点,然后就可以把整棵树给实现出来
那么,你可能要问了,这玩意有啥用么
你不觉得这个看起来很像 传* 嘛
hhhh好了好了,这个其实在系统中也有用到
就是UNIX和DOS中的目录结构
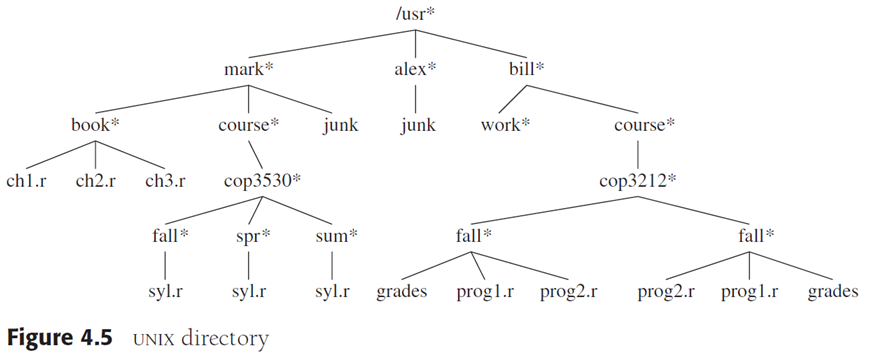
这里有三个小名词
preorder traversal 先序遍历
postorder traversal 后序遍历
inorder 中序遍历
这玩意一般都会出现在二叉树里面
你要不懂啥叫二叉树的话
诺
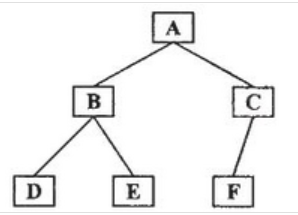
这就是二叉树
所谓先序和后序,不过是开始的位置不一样罢了
这样吧,你看上面那张座机像素的图,我给你讲讲
先序遍历结果:ABDECF
中序遍历结果:DBEAFC
后序遍历结果:DEBFCA
结合先后顺序看看就很容易地可以看懂啦
嘿,我们好像还没讲二叉树!
我们回过头来看看啥叫二叉树
二叉树 Binary Tree 是任何节点有两个后继节点以内树
简单来说就是
树节点的声明在结构上与双向链表的声明还是很相似的,因为该结构可以由元素信息加上两个其他节点的对应信息来使用,用人话来概括就是:

这里面有两个小玩意,操作数和操作码
Operands 操作数 是表达式的叶子的数量
Operators 操作码 比如运算符
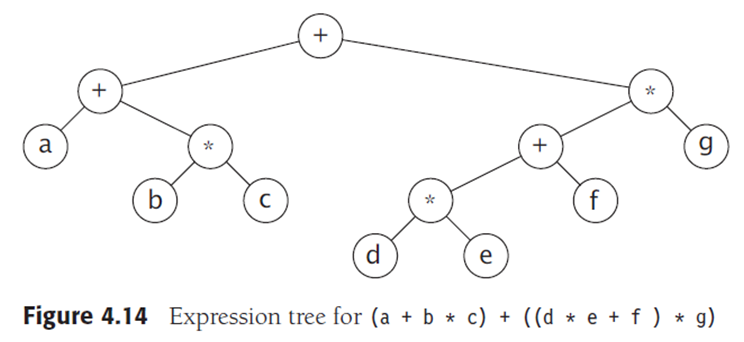
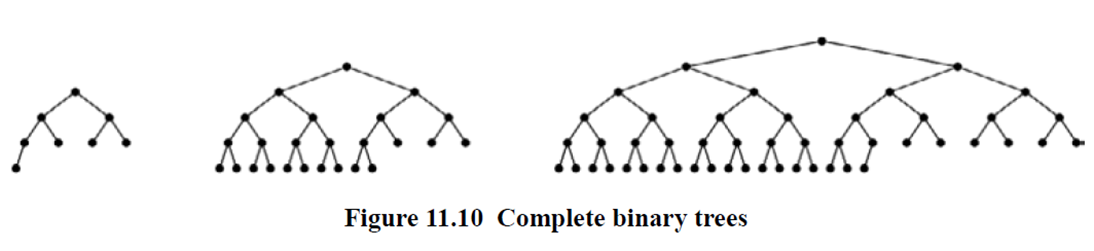
所谓的全二叉树,就是二叉树的所有叶子都在同一级并且都含有两个子节点,我们称之为全二叉树
高度为H的二叉树有 L = 2h 个叶子和 M = 2h -1 个内部节点,
高度为h的完整二叉树共有n = 2^(h + 1) – 1个节点
完全二叉树既可以是全二叉树,也可以是右侧缺少一部分叶子的全二叉树。其他都和全二叉树所差无几
先不要看答案(我估计这个图你不点开肯定看得不太清),试试把下面的这个式子转换为全二叉树
a b + c d e + * *
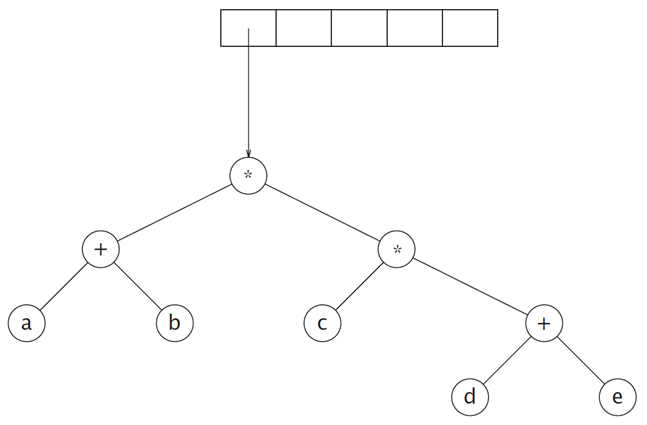
假如,从右边开始,我们每一次都读一个符号,并将其压进栈之中
那么一个一个来的话对应的应该是
a b + c d e +
二叉树一个很重要的用途就是用来搜索 search
二叉树变成 二叉搜索树 binary search tree 的属性就是对于树中的每一个节点 X, 每一行 左边的所有项目 left subtree都小于X,右边的项目都大于 right subtree X
同时我们会假定所有项目都是不一样的,然后后序再处理重复的项目
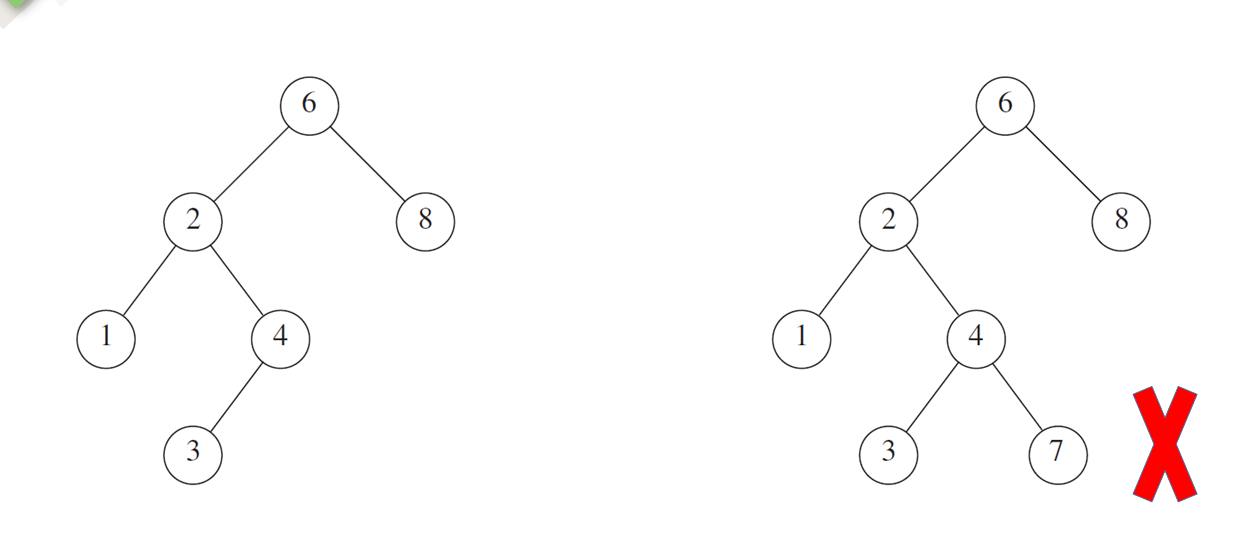
上面这里需要着重讲一下下
你看为什么这个7错误了呢?
你看7是不是比根 6 要大
那么它应该在6的右边
可以说一个新的元素进入树的时候,我们会挨个儿查看
首先先看根,如果根这边ok了的话,再往下推
所以简而言之,这个定理适用于根,也适用于每一篇有后继的叶子(每一个子树)
反正我感觉这种定理单用文字还是很难理解的,关键是要结合上面这个图去理解
思考一下为什么7放在这里是错误的
哦对了,二叉搜索树要求所有项目都可以自定义
所以在编写此类代码的时候,一般都会预留一个可以自定义的接口类型,

诶,那么这个时候,有问号可能有同学了,我们要怎么去搜索指定的元素呢?
你之前说的这个东西是用来排序的,那么调用的时候要用一个什么样的思路呢?
别急,我们先来看一个图
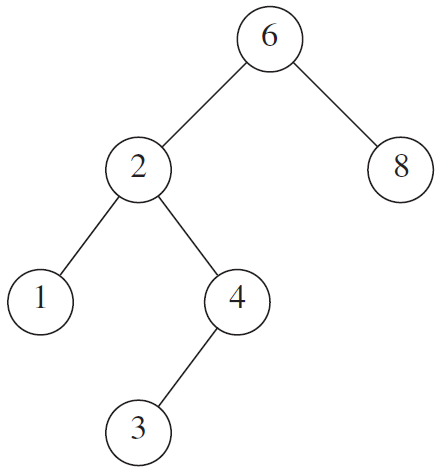
如何在上面这个图中快速地找到 4 这个元素呢?
首先我们先来讲讲大概的思路: 当树中的一个节点含有我们需要的元素的时候,返回True,否则返回False
你看这个树不是很多节点嘛,那一个一个找就好了嘛
算法:
- 如果需要找的节点等于根,那么搜索成功
- 如果需要找的节点小于根,那么搜索左子树,否则搜索右子树
- 如果需要找的节点大于右子树,那么搜索右子树
以此类推
这里的算法思想可不是循环哦!
这里的思想是递归!
如果你问我啥时递归,往上翻翻吧~
在之前讲过递归的概念
那么相对的,添加元素也是类似的做法
比如我们需要在正确的位置添加元素 5
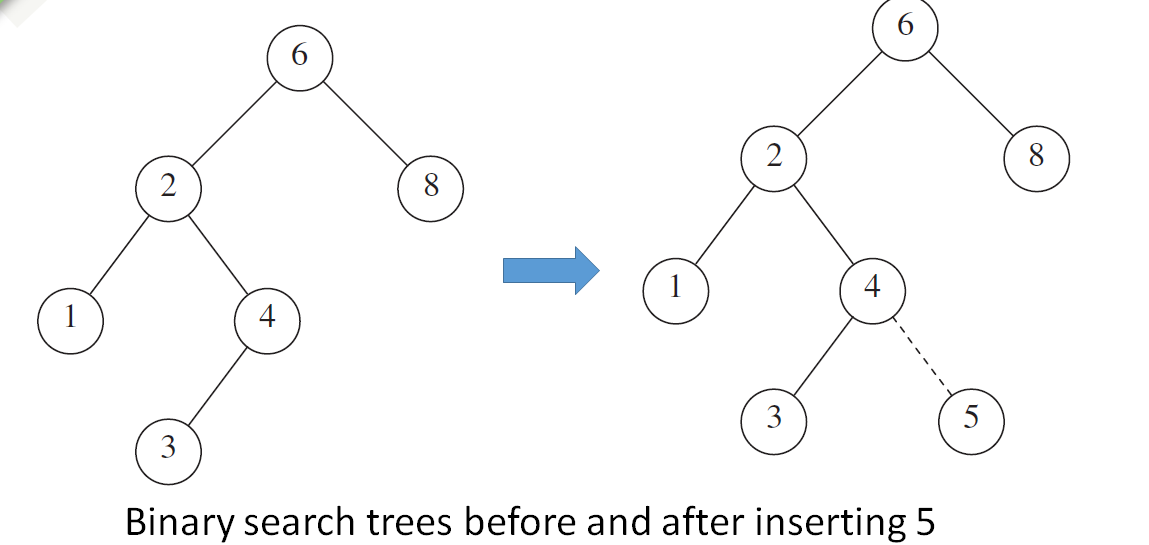
如果我们需要添加的节点小于根,那么:
如果有子树,则向左走,若没有,在此处添加
如果需要添加的节点大于根,那么:
如果有子树,向右走,如果没有子树,在此处添加
说白了还是一个if else 语句
嗯说完了添加,我们来聊聊删除
在前面先说一下,所有的节点,除了是末端的叶,其他的都不能直接删除
一定要更改指向(继承关系)后才可以删除
不然会导致树的混乱
其实在树中删除元素,并不是真正的删除掉,只是改变了其指向罢了
不过这个也分情况
当这个节点是叶子的时候,可以将其立刻删除,这种删除就是真正的删除了
但是这个节点有一个子节点的话,可以在其父节点调整节点之间的连接,绕过该节点,就实现了删除的操作
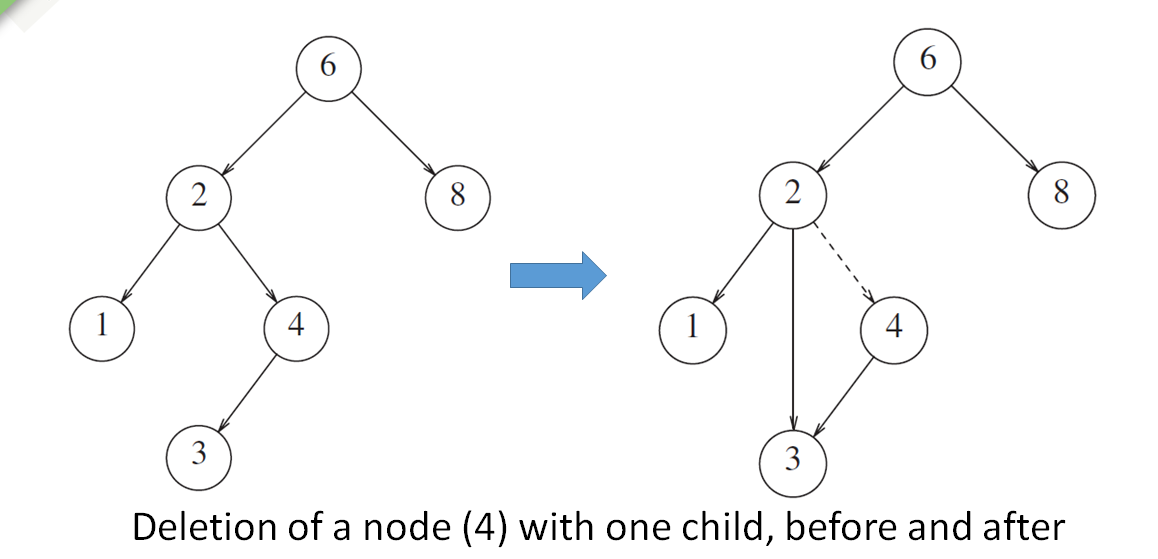
那你有没有想过,如果需要删除的节点之下也有一个小节点呢?
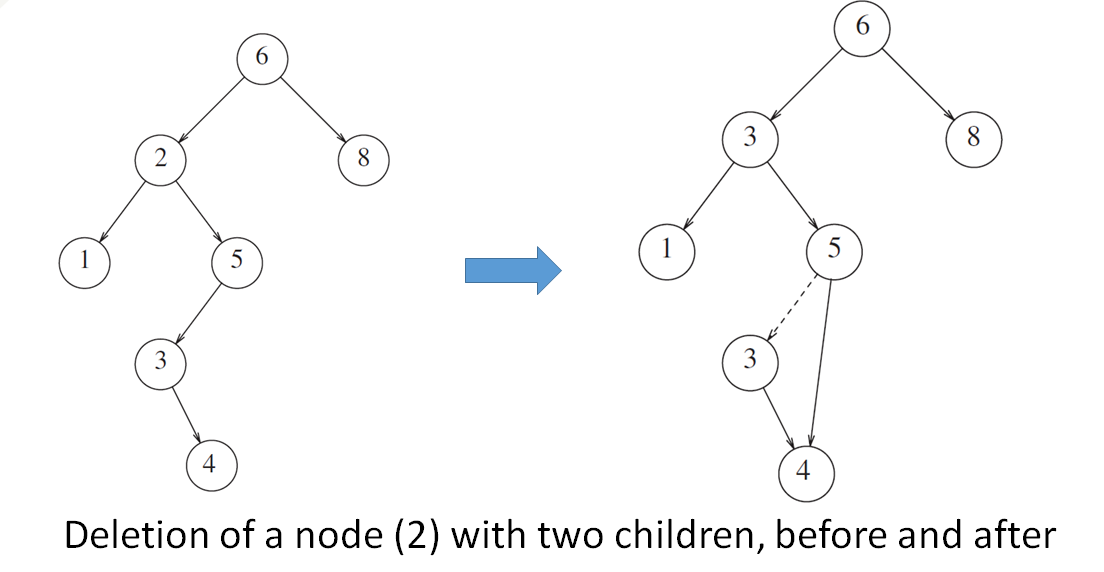
一般来说,我们可以直接把节点给替换掉,就像上图中的那种操作
同时也因为右子树中的最小节点不能是左子节点,所以可以很方便地直接替换
那我们不难总结出: 当我们要删除节点的时候,
- 如果该节点是叶,那就可以立刻将其删除
- 如果该节点有一个子节点,就可以将其子节点直接继承父节点实现删除操作,后续将其删除即可
- 如果该节点下有一个父节点和一个子节点,最好的方法就是使用子树最小的数据直接替换该节点的数据(更改指向),然后我们需要删除的这个节点就没了指向,就是空节点,可以将其直接删除
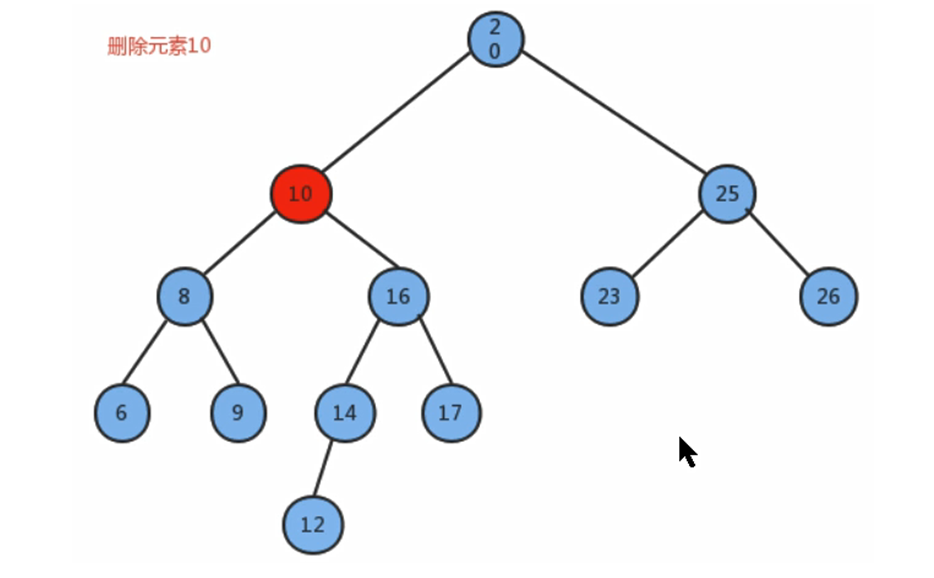
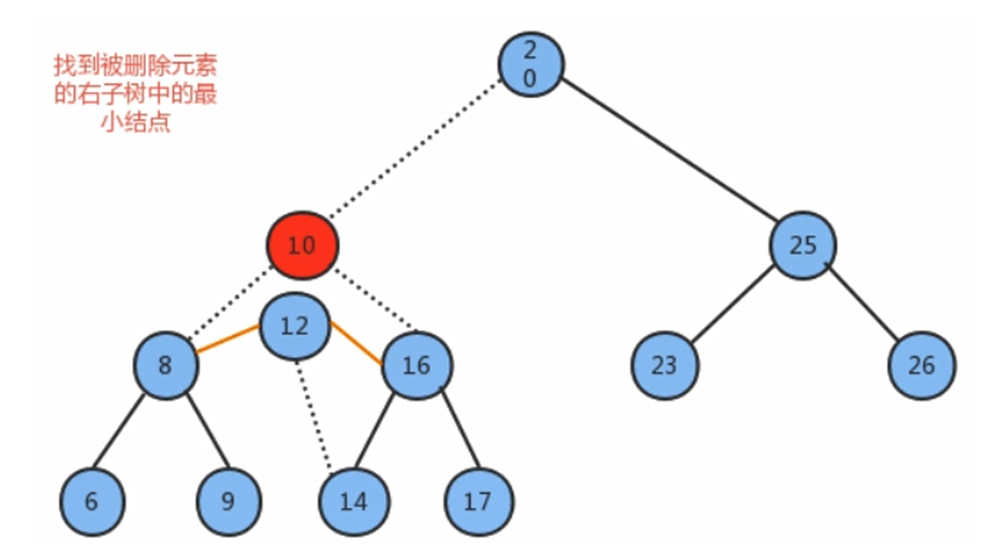
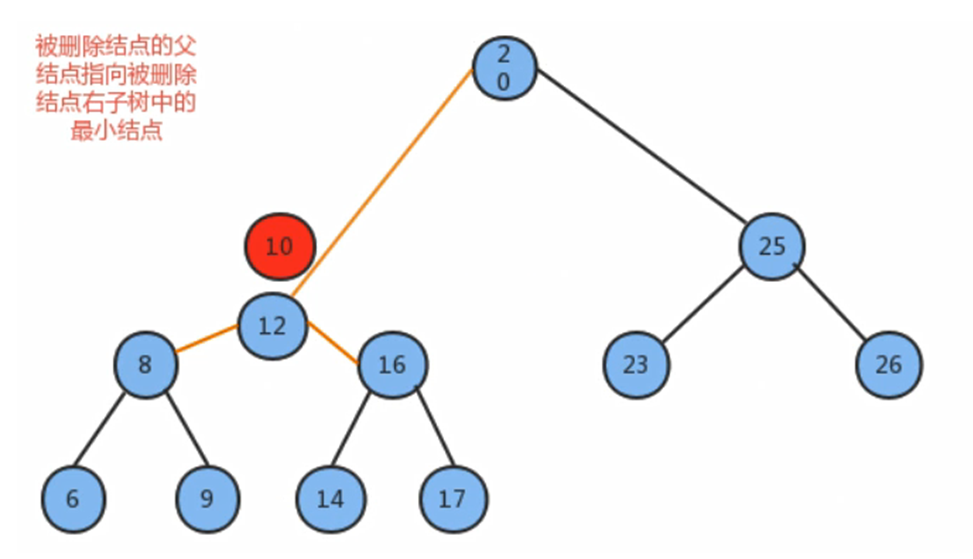
二叉树的增删查改,都使用了递归的思想
不仅仅是简单的if else
哦对了,你知道树的中序遍历 in-order traversal 吗
这个是先访问左子树,然后是根节点,再到后子树
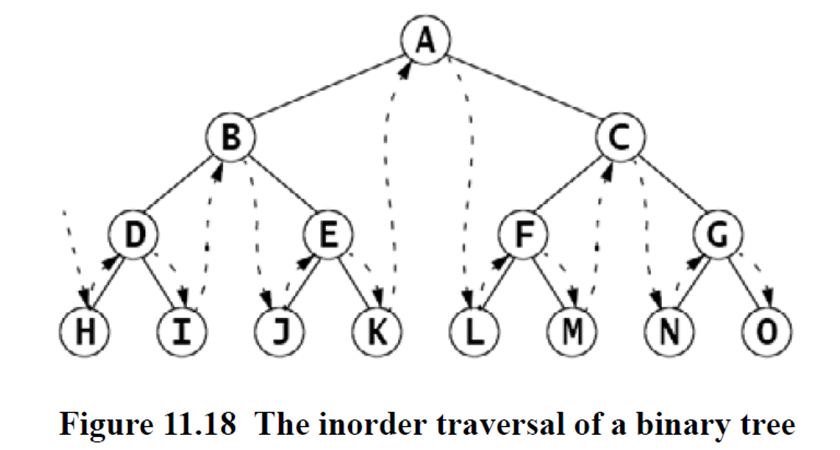
当然,除了有序遍历之外,我们还有
Pre-order traversal
Post-order travsersal
Level-order traversal

你看上面这个程序就是递归
嗯,下面我们进入下一章,集合和映射 Set and Map
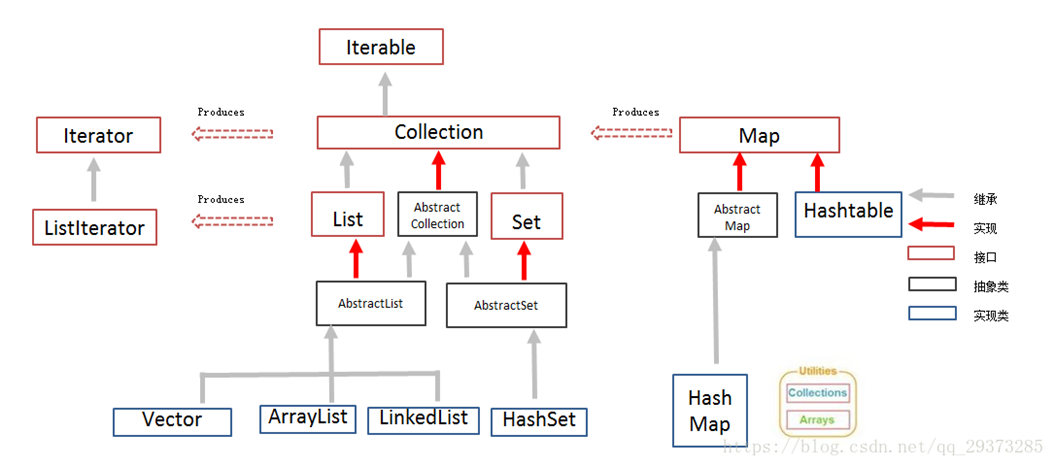
Set继承于Collection接口,是一个不允许出现重复元素,并且无序的集合,主要有HashSet和TreeSet两大实现类。
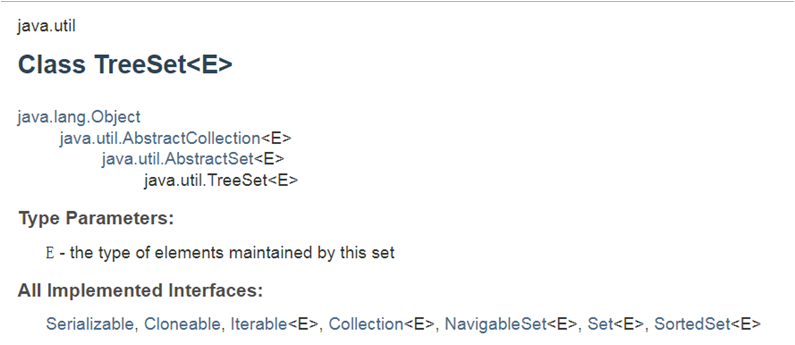


Map 接口中键和值一一映射. 可以通过 键 keys 来获取 values 值 。
同时,TreeMap是SortedMap的一种实现。
TreeMap 由红黑树实现,可以保持元素的自然顺序,或者实现了 Comparator 接口的自定义顺序
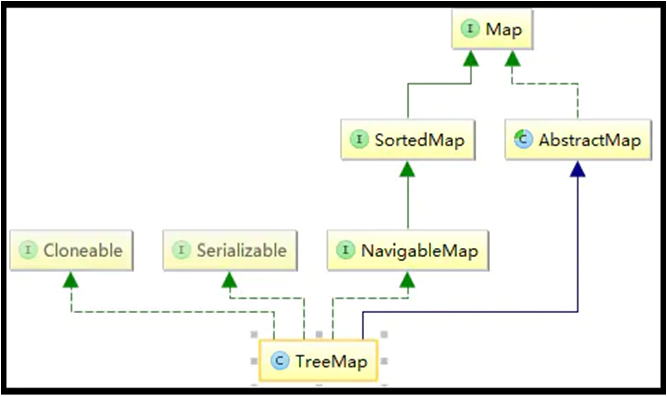

关于使用TreeMap,我们有:
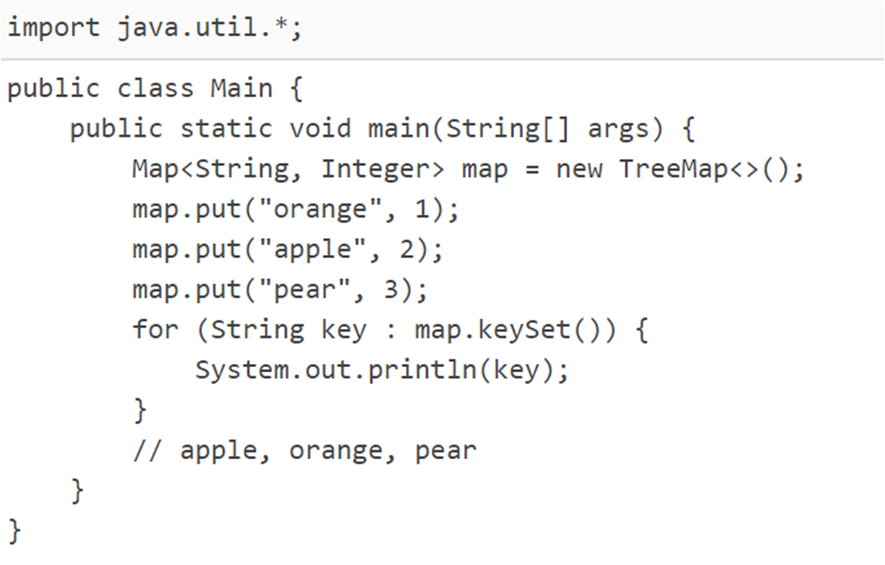
什么?你说我为啥啥也没说?
因为有一个神仙网站
https://www.liaoxuefeng.com/wiki/1252599548343744/1265117109276544
或者你也可以使用按钮一键前往
Chapter 5 : Hashing
哦哦哦哦哦哦哦~他来了!
哈希!
嘿嘿
这玩意以前就听过,感觉挺厉害的
但是它确实是挺厉害的(小声BB)
那咱们先来看一下哈希的定义吧

嘛,其实 哈希表 Hash table 的实现通常叫做 哈希 Hashing
哈希是一种用于在 常量的平均时间内 constant average time 执行 插入 insertions,删除 deletions, 搜索 searches 的技术
一个理想的哈利表的数据结构应该是一个包括其中 项 items 在内都是 固定大小 fixed size 的 数组 array
我们一般把其中的元素称之为值 value, 我们使用 Key 来生成唯一的值
哦对了,你听过Hash Function 嘛?
当我们把每个键都映射在 0 到 TableSize - 1 这个范围中,并且放置在适当的格子中的时候,那么这个映射就被称之为 Hash Function 散列函数
在理想状态下,这个函数有着易于计算的特点,并且可以确保两个不同的键都会放在不同的格子中
这个时候有一个小问题,如果两个键有着同样的值呢?
嘿嘿,盲点发现了华生!
我们把有着两个相同函数值的情况称之为 collision 冲突,当函数值冲突的时候,选择适当的表格就显得尤其重要了
那么,我们可以大概地总结其Hashing Mechanism 散列机制
- 用来存储数据的一个数组结构咱们称之为哈希表格
- 基于哈希键值,将数据插入哈希表格中
Hash Key Value / Hash Code 哈希键值,哈希表
- 哈希键值是一个特殊的值,用作数据项的索引
- 它指示数据项应储存在哈利表的中的位置
- 我们一般使用哈希函数生成哈希键值
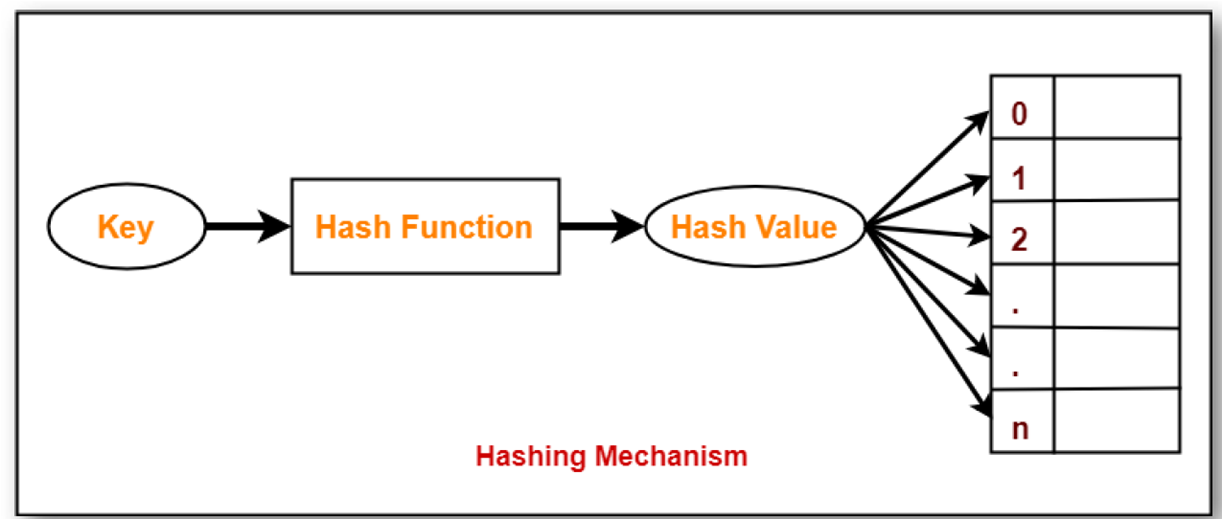
下面咱们着重来看看哈希表吧
哈希表是使用特殊功能从其键值计算数据值的位置,不是计算储存值的方法啊啊啊!
哦?你说啥时特殊功能?
这个就是 hash function 散列函数
在Java中,在java.util中有一个特定的Hashtable类,但是它实际上只是一个HashMap类罢了
- 散列函数采用一组特定的字符(我们将其称之为键),并将其映射到一定长度的值上面(我们将其称之为哈希值/哈希)
- 一般来说,这玩意算起来都挺简单的
- 哈希值应该平均分配
- 减少重复 collision
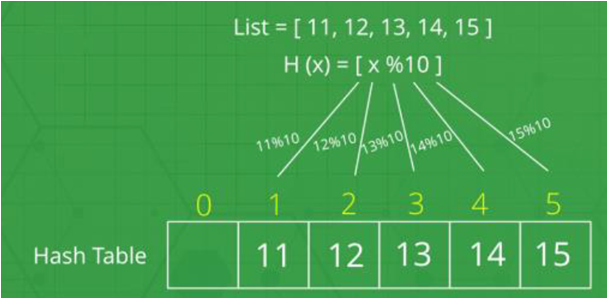
假如我们有一组数字,分别是 54, 26, 93, 17, 77, 31.
那我们可以使用“特殊方法”将其储存起来
比如这里我们可以使用 余数方法
别告诉我你不知道啥是余数
要不这样吧,假如 h 是上面几个数字中的随机一个,那么我们应该有
(注意这里的 size of table 是11)

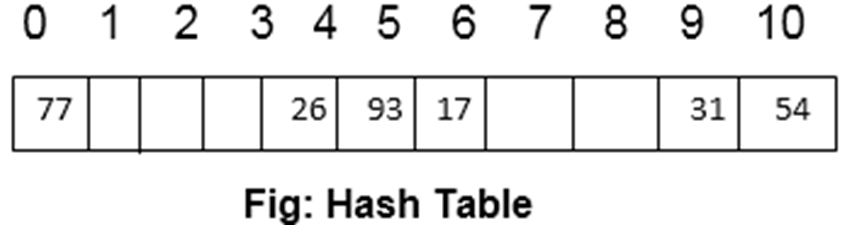
嗯,你也看到了,对于任意的数字,如果按照上面的“特殊方法”储存起来的话,只需要按照它的余数来储存数据就可以了
那么反过来,当我们搜索数据的时候,只需要将这个数据求余,然后再根据余数来找,就很方便啦 那么在这里总结其搜索时间的话,应该为O(1)
但是,你有没有想过,万一两个数字放进了同一个方框里面呢?
嘿嘿,那就很麻烦了对吧
因为我们并没有相关的查找方法来查找里面的元素
所以这种东西我们将其称之为 collision 冲突
Loading factor 装填因子 指 (哈希表储存元素的大小 / 表的大小) ,是一个比值。 假如这个比值是1,那么说明这个表已经被装满了,下一个元素必定会冲突。
所以我们一般都会设定一个值,一般是0.7, 当装填因子达到0.7的时候就对哈希表进行扩容以避免冲突
嗯,或许你也在想有没有什么方法,这里可以先给一个概括图
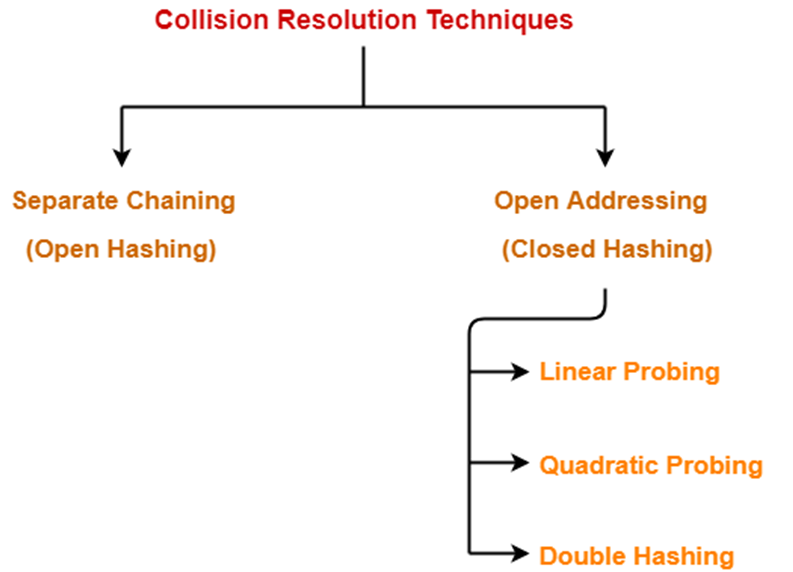
为了解决上面这个问题,我们有:分离链接法 Separate Chaining
emmm我也懒得用言语去描述了
直接上图
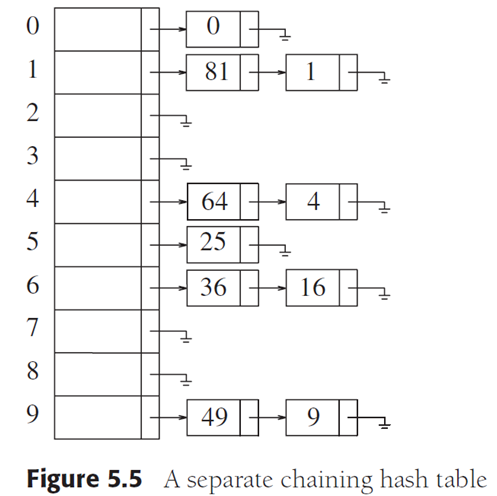
举个栗子,我们现在有 0 1 2 3 4 5 6 这7个盒子,然后我们有几个数字需要储存起来
50, 700, 76, 85, 92, 73 and 101
在这里我们就可以很好地使用 分离链接法来储存数据
首先,我们需要先绘制一个哈希表格,因为我们有7个盒子,所以使用的应该是像下面这样的哈希表格








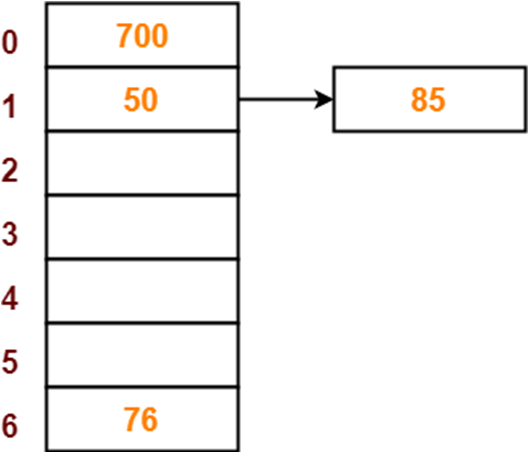

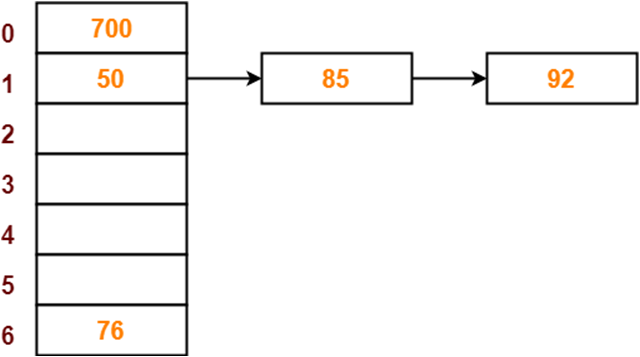

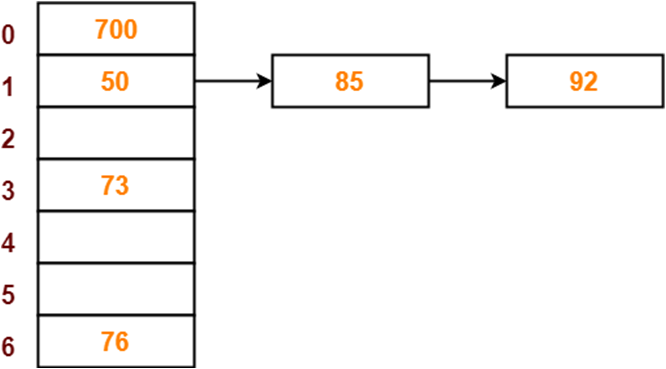

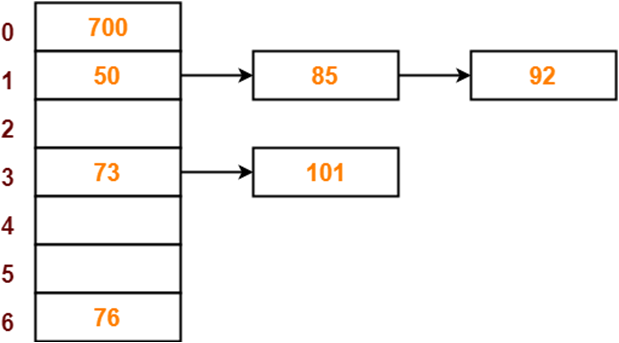
嗯,反正我是感觉直接一串图比我打一对的字要更容易理解(摊手)
那么,除了上面的分离链接法之外,还有没有其他的方法呢?答案是肯定哒
Open Addressing 开放地址法
Linear Probing 线性探测
Quadratic Probing 平方探测
Double Hashing 双散列
Rehashing 再散列
哦吼吼吼吼,女士们先生们,下面让我们有请线性探测先生上台!
“啪啪啪啪啪啪”
其实这玩意理解起来倒是挺简单的
就是依次搜索每一个单元格以找到空的单元格,然后将数据丢入其中


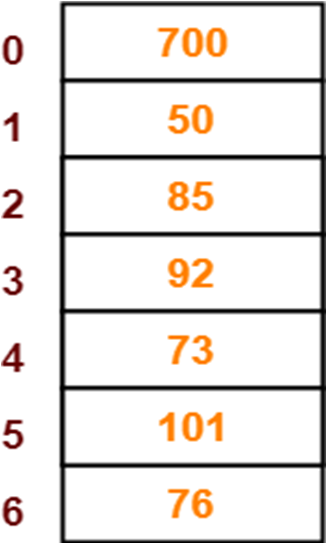
嗯,你看上面的图中,700和50就处在了应当的位置,但是85却往下移了一位
这也就是线性探测的意思
如果当前“茅坑”有人了,就会自动前往下一个没人的茅坑
这里有一点需要注意一下,平方探测是一种冲突解决方法
准确地来说就是它会消除线性探测的 主聚类 primary clustering 问题
一般都流行一道公式
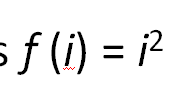
具体怎么用呢?来看个例子吧



你看,当某个“茅坑”已经满人的时候,就会根据这种操作去寻找下一个茅坑
(hash(x) + 1*1) % S
比如你看第一个,76 % 7 = 6,所以就放进了6这个格子里面
40 % 7 = 5
48 % 7 = 6,这里注意,这个时候和前面的76冲突掉了
所以这个时候55就会加到上面的这个公式里面,寻找另一个茅坑
(48 + 1) % 7 = 0 ,这样就会自动将其放入 0 当中
注意这里的 i 指 1 2 3 4 5这一类的常数
一般我们也只用1的平方以及2的平方之类的
在这里纪念 404 的Chapter 6
R.I.P
Chapter 7: Sorting
吼吼吼!排序!
诶之前啥时候做过排序来着
不知道为啥感觉这玩意之前好像做过
OOOOOO对了!之前疫情时候的网课有讲过这个!
还是气泡排序感觉最可爱
因为!bubble!!!
就有一种嘟噜噜噜噜的感觉~
嘛~排序的定义嘛,只需要记得这玩意就是把数字从大到小排序号就够了
什么性质啊这些乱七八糟的
emmmm
如果你想的话当然也可以记啦
不过我感觉这东西还是实用性为主
记得怎么用还是比较靠谱一点
首先,我们先来看我最喜欢的-气泡排序 bubbbbbbbbbbbbbble!
嗯,我也弄不懂我为啥现在才发现这个网站
这个网站真的太棒了
并且,它还有中文版本的
虽然是机翻,但是还是很不错的
https://visualgo.net/zh/sorting
它上面使用动态的示例图来展示排序
或者你也可以点击按钮快速前往
在这里吐槽一下右下角的这个玩意

诶唷,啥叫机翻啊
那个“做”真的是搞死我了
看得头疼
哦对了在上面的这个网站里面还有
selection sort 选择排序
Insertion Sort 插入排序
记得一起看看啊
我就不写出来了,因为那种可视化的动图真的太好理解了
一定要去看啊!!!!!!
Chapter X: Searching
快把chapter6的棺材板按住
嗯这一个章节我们来看看怎么搞搜索
关于搜索的定义嘛,真的不想再说了
dddd
在这里主要讲两种搜索方法:
Linear (Sequential) Search 线性查找法(又称顺序查找法)
Binary Search 二元搜索
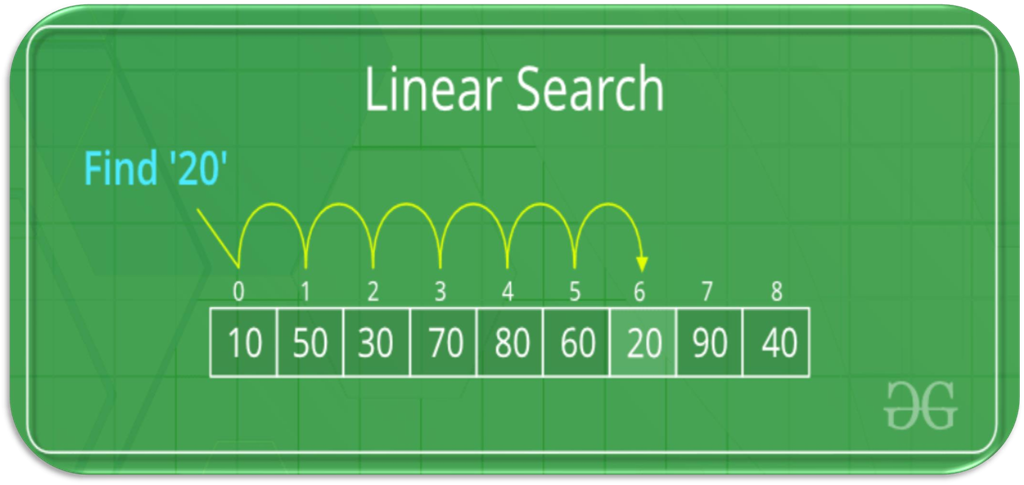
在这里贴出一个算法概括,采用机器翻译的方法
Step 1 - Read the search element from the user.
Step 2 - Compare the search element with the first element in the list.
Step 3 - If both are matched, then display "Given element is found!" and terminate the
function.
Step 4 - If both are not matched, then compare search
element with the next element in the list.
Step 5 - Repeat steps 3 and 4 until search element is compared with last element in the list.
Step 6 - If last element in the list also doesn't match, then display "Element is not found!" and terminate the function.
第1步-从用户那里读取搜索元素。
第2步-将搜索元素与列表中的第一个元素进行比较。
步骤3-如果两者都匹配,则显示“找到给定的元素!” 并终止该功能。
步骤4-如果两者都不匹配,则将搜索元素与列表中的下一个元素进行比较。
步骤5-重复步骤3和4,直到将搜索元素与列表中的最后一个元素进行比较。
步骤6-如果列表中的最后一个元素也不匹配,则显示“找不到元素!” 并终止该功能。
如果把它搞成代码的样子,那大概就是这样子的

我还是感觉结合图来理解的话可以更快一点
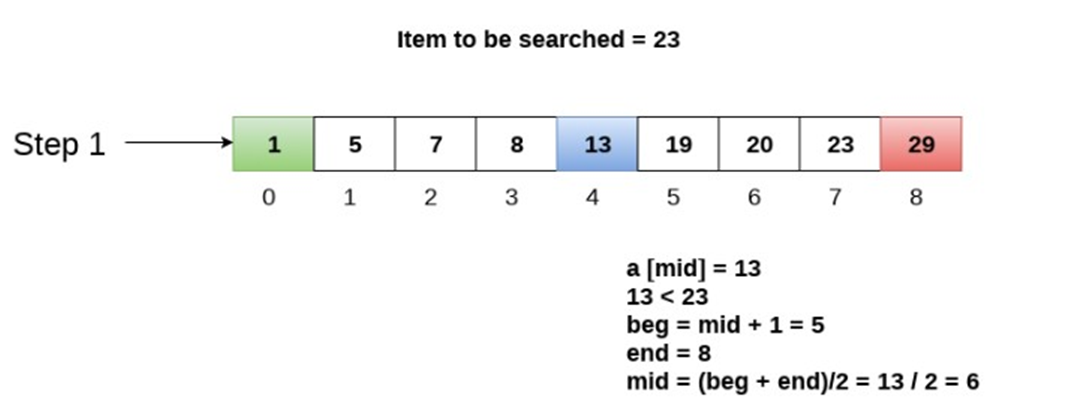
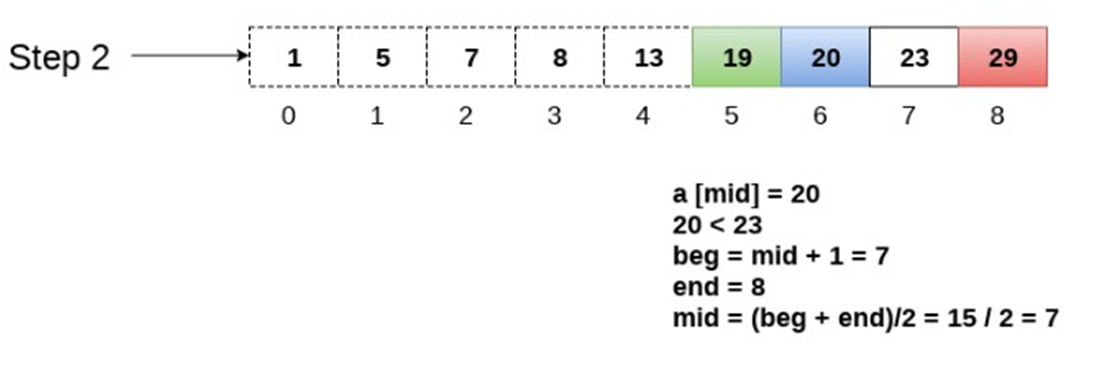
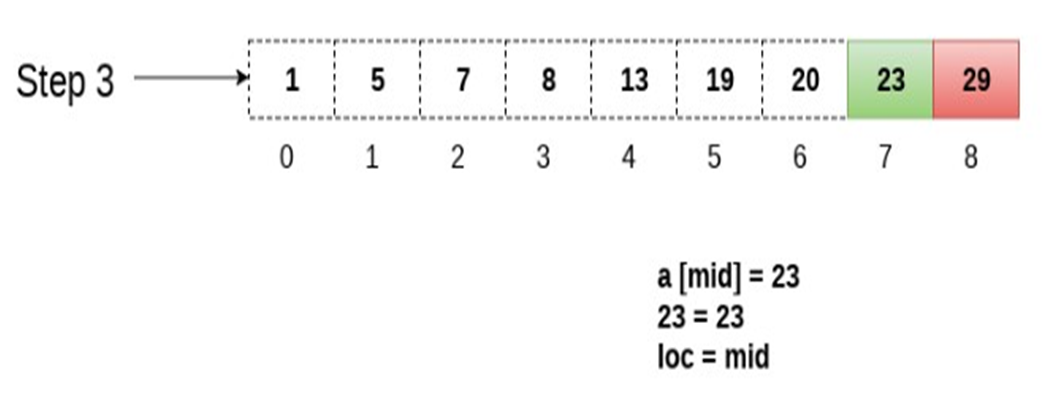
嗯,为啥咱们要学这个咧?
因为这个二元搜索法是一种很好的搜索技术
当所有元素都按照顺序排序的时候
它可以快速地将这个元素与列表中间的元素做一个比较
然后就可以将列表分成一般来搜索
这样就像是一半一半地来了
对于大型的数据库之类的尤其的好用
如果用代码实现的话,大概就是:

还是老样子,用视频去理解
https://www.bilibili.com/video/BV1UE411N71D
我感觉这个视频虽然挺简单的,但是很好地说明了希尔排序的算法,我觉得这个就够了
这里需要注意的是,一般我们都会从大的间隔往小的间隔去排序
不可能一上来就是大间隔
一般来说,我们都是
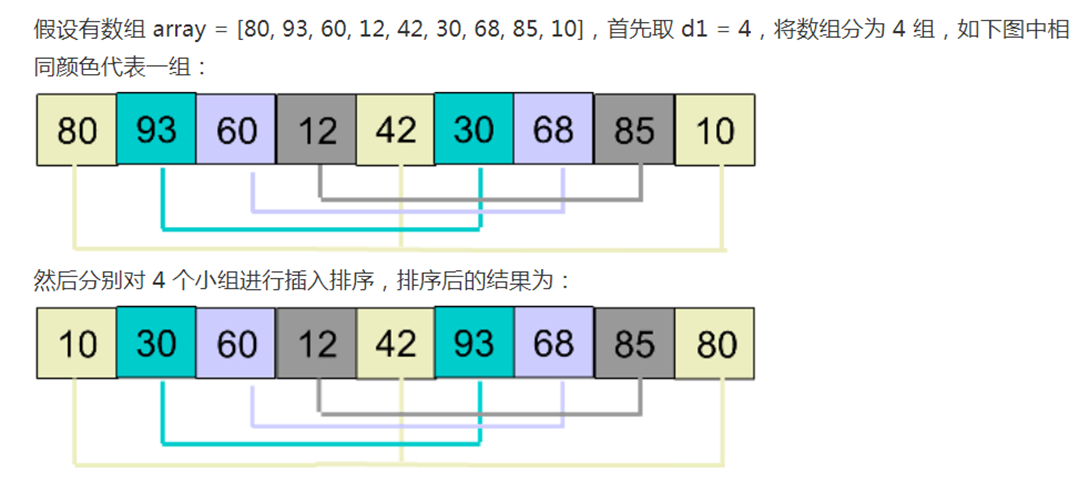
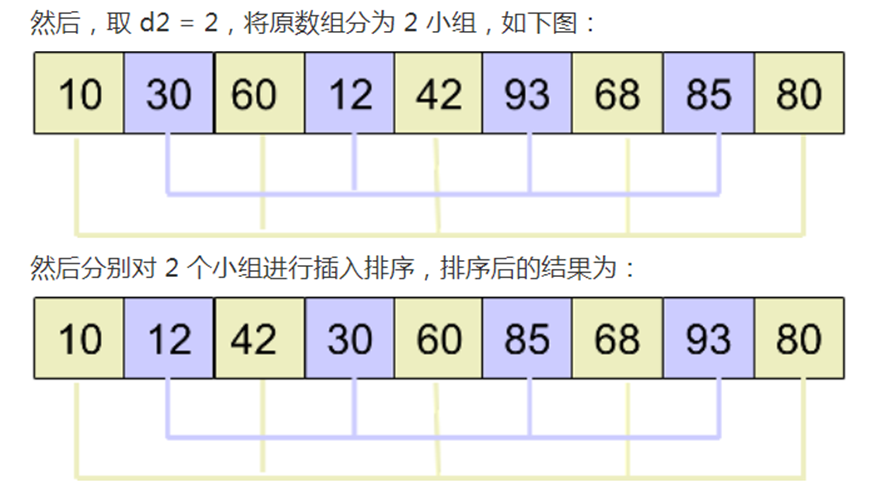
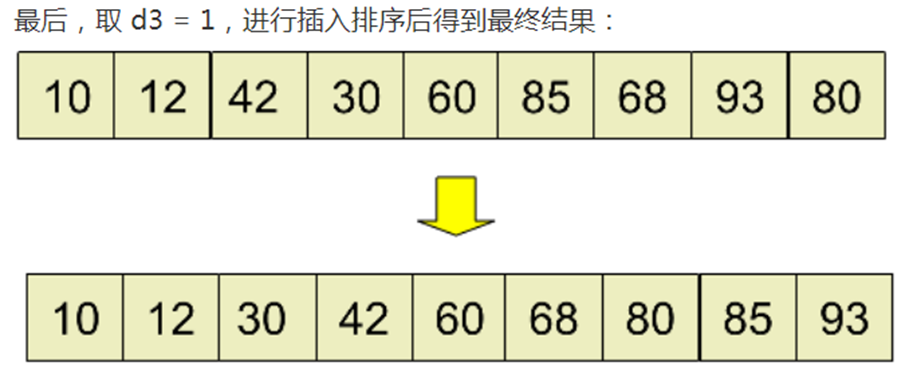
可见,我们从d1开始,到了d3就选择了整个数组
这个是因为数组比较小的原因
当对于那种复杂一些的数组的时候,就能够体现出这个排序的优越性了
哦对了,之前忘了说一下
就是我之前安利的那个网站
这里
可以选择不一样的排序方式
这里面也包括了这次的并归排序

一般来说,并归排序体现了一种思路:分而治之 Divide and Conquer
嘛,我就不用文字来表达定理了
这玩意写起来真的是太麻烦了
并且效果还不如放一张动图
诶奇了怪了,为啥动不起来
算了还是自己去网站上看看吧
就是之前安利的那个小网站
看这个并归排序的时候记得把速度放慢一点
感觉这玩意速度好快
还有,这玩意虽然体现了分而治之的概念,但是这其中也有汇总到一起的概念
用图来概括的话大概就是

天呐,这玩意看起来都好烦人,还得一个一个加上去
不得不说cc做PPT真的好用心
这里可以看到,这个是先把数列拆开,然后在合并起来
就是逐个击破的意思吧
emmmmm......这玩意真的排的快吗
感觉好麻烦啊
(:з」∠)
首先,记得去看看视频理解一下
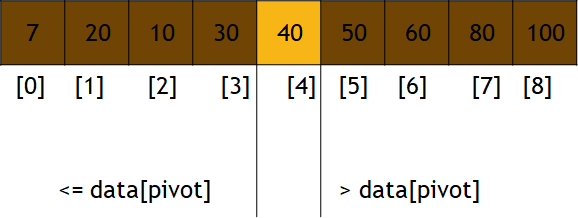
其次,这里用于做比较的是 pivot_index ,也就是那个橘黄色的方块
往后的每一个方块都是在和这个橘黄色的方块作对比
比较核心的一行代码就是这个swap(i, storeIndex); storeIndex++
也就是说,当我们每遍历一次数组的时候,至少会将1个数字排列到它们应该处在的位置
并且可能还排列到更多的数字
记得一定要去网站上仔细的看,速度放慢一点
这个真的是不好理解
本章节末:不同算法的时间复杂度